Condensador cilíndrico e método das imagens simétricas

Expandir

Metadata

• CONTEXTO : Primeiro ciclo universitário
• AREA: Física
• DISCIPLINA: Eletromagnetismo e Óptica
• ANO: 2
• LINGUA: pt
• AUTOR: Jorge Loureiro
• MATERIA PRINCIPAL: Eletrostática na matéria
• DESCRICAO: Determinação do campo elétrico máximo e da capacidade de um condensador. Determinação da diferença de potencial máxima entre as armaduras. Determinação da densidade de carga induzida através do método das imagens simétricas.
• DIFICULDADE: *****
• TEMPO MEDIO DE RESOLUCAO: 20 min
• TEMPO MAXIMO DE RESOLUCAO: 40 min
• PALAVRAS CHAVE: campo elétrico, condensador, dielétrico, potencial, Poisson, cilindro, imagens, simétricas, plano

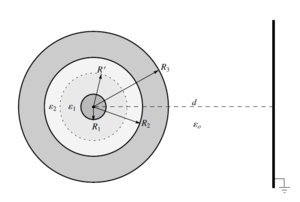
1. A figura representa um condensador cilíndrico ideal (comprimento $\gg$ diâmetro) com armaduras condutoras de raios $R_1 = 2\text{ mm}$, $R_2 = 8\text{ mm}$ e $R_3 = 10\text{ mm}$. O espaço entre as armaduras está completamente preenchido com dois materiais dielétricos de permitividades diferentes: $\epsilon_1 = 4\, \epsilon_0$ entre $R_1$ e $R'$, e $\epsilon_2 = 2\, \epsilon_0$, entre $R'$ e $R_2$, sendo $R' = 4\text{ mm}$. As densidades de carga por unidade de comprimento nos condutores interior e exterior são, respetivamente, $\lambda_1 = 0.1 \: \mu\text{C.m}^{-􀀀1}$ e $\lambda_2 = 0.2 \: \mu\text{C.m}^{-􀀀1}$.
   1. Determine nestas condições o campo elétrico máximo em cada dielétrico e a capacidade, por unidade de comprimento, do condensador.
   2. Assumindo que o campo de rotura em ambos os dielétricos é $E_{rot} = 200\text{ kV.cm}^{-􀀀1}$ (ou seja, a partir deste valor os dielétricos deixam passar corrente), determine a diferença de potencial máxima entre as armaduras para a operação normal do condensador.
2. Considere agora que este condensador é colocado paralelamente a um plano condutor infinito, ligado à Terra, a uma distância $d$ do seu eixo. Determine a densidade de carga do plano nos pontos mais próximos do cabo coaxial. Apresente os resultado em função das densidades de carga $\lambda_1$ e $\lambda_2$ , não necessitando de realizar qualquer concretização numérica.