Diferenças entre edições de "Matriz da transformação de um paralelogramo"
| Linha 17: | Linha 17: | ||
</div> | </div> | ||
| − | Considere a aplicação linear \(T\) de \( \mathbb{R}^2 \to \mathbb{R}^2 \) que transforma o paralelogramo da figura | + | Considere a aplicação linear \(T\) de \( \mathbb{R}^2 \to \mathbb{R}^2 \) que transforma o paralelogramo da figura à esquerda no da direita, sendo cada triângulo levado no correspondente triângulo da mesma cor. Qual das seguintes é a matriz da transformação \(T\)? |
[[File:Before.gif]] | [[File:Before.gif]] | ||
[[File:After.gif]] | [[File:After.gif]] | ||
Revisão das 23h17min de 1 de novembro de 2016
Metadata
- CONTEXTO : Primeiro ciclo universitário
- AREA: Matemática
- DISCIPLINA: Álgebra Linear
- ANO: 1
- LINGUA: pt
- AUTOR: Ana Moura Santos e João Pargana
- MATERIA PRINCIPAL: Transformações lineares
- DESCRICAO: matriz da transformação em R2
- DIFICULDADE: ***
- TEMPO MEDIO DE RESOLUCAO: 15 mn
- TEMPO MAXIMO DE RESOLUCAO: 30 mn
- PALAVRAS CHAVE: matriz canónica, matriz da transformação, transformação linear, imagem da transformação, transformado
Considere a aplicação linear \(T\) de \( \mathbb{R}^2 \to \mathbb{R}^2 \) que transforma o paralelogramo da figura à esquerda no da direita, sendo cada triângulo levado no correspondente triângulo da mesma cor. Qual das seguintes é a matriz da transformação \(T\)?
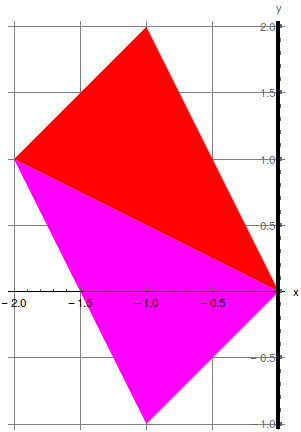
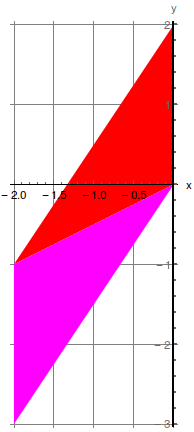
A) \(\left(\begin{array}{cc}\frac{4}{3}&\frac{2}{3}\\\frac{4}{3}&\frac{5}{3}\\\end{array}\right)\); B) \(\left(\begin{array}{cc}\frac{2}{3}&-\frac{2}{3}\\-\frac{1}{3}&\frac{7}{3}\\\end{array}\right)\); C) \(\left(\begin{array}{cc}\frac{4}{3}&\frac{4}{3}\\\frac{2}{3}&\frac{5}{3}\\\end{array}\right)\); D) \(\left(\begin{array}{cc}\frac{2}{3}&-\frac{1}{3}\\-\frac{2}{3}&\frac{7}{3}\\\end{array}\right)\).
Para obter o zip que contém as instâncias deste exercício clique aqui(repmat_variante_2)
Se deseja obter o código fonte que gera os exercícios contacte miguel.dziergwa@ist.utl.pt