Diferenças entre edições de "Rotação de um quadrado fora da origem"
Saltar para a navegação
Saltar para a pesquisa
| Linha 16: | Linha 16: | ||
</div> | </div> | ||
</div> | </div> | ||
| − | Considere a seguinte rotação em \(\frac{\pi}{2}\) radianos do quadrado mais claro em torno do ponto \(\left | + | Considere a seguinte rotação em \(\frac{\pi}{2}\) radianos do quadrado mais claro em torno do ponto \(\left[\begin{array}{c}1\\1\\\end{array}\right]\), que resulta no quadrado mais escuro. |
[[File:Rotation.gif]] | [[File:Rotation.gif]] | ||
Revisão das 23h20min de 1 de novembro de 2016
Metadata
- CONTEXTO : Primeiro ciclo universitário
- AREA: Matemática
- DISCIPLINA: Álgebra Linear
- ANO: 1
- LINGUA: pt
- AUTOR: Ana Moura Santos e Miguel Dziergwa
- MATERIA PRINCIPAL: Transformações lineares
- DESCRICAO: rotação de um quadrado fora da origem
- DIFICULDADE: ***
- TEMPO MEDIO DE RESOLUCAO: 20 mn
- TEMPO MAXIMO DE RESOLUCAO: 30 mn
- PALAVRAS CHAVE: transformação linear, coordenadas homogéneas, rotação fora da origem, translações, composição de transformações
Considere a seguinte rotação em \(\frac{\pi}{2}\) radianos do quadrado mais claro em torno do ponto \(\left[\begin{array}{c}1\\1\\\end{array}\right]\), que resulta no quadrado mais escuro.
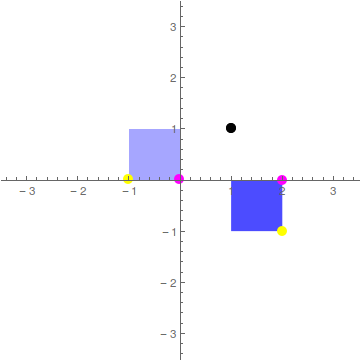
Indique a matriz responsável por esta rotação.
A)\(\left(\begin{array}{ccc}0&-1&2\\1&0&0\\0&0&1\\\end{array}\right)\), B)\(\left(\begin{array}{ccc}0&1&0\\1&0&0\\0&0&1\\\end{array}\right)\), C)\(\left(\begin{array}{ccc}0&-1&-2\\1&0&0\\0&0&1\\\end{array}\right)\), D)\(\left(\begin{array}{ccc}0&-1&1\\1&0&1\\0&0&1\\\end{array}\right)\)
Para obter o zip que contém as instâncias deste exercício clique aqui[1]
Se deseja obter o código fonte que gera os exercícios contacte miguel.dziergwa@ist.utl.pt