Diferenças entre edições de "Experiência de Thomson"
| Linha 155: | Linha 155: | ||
==Efeitos da corrente eléctrica estacionária criada por uma espira== | ==Efeitos da corrente eléctrica estacionária criada por uma espira== | ||
| + | [[file:fig-fio.jpg|thumb|upright=0.5 |alt=Campo magnético produzido por um fio onde passa corrente |Campo magnético produzido por um fio onde passa corrente]] | ||
| + | [[file:fig-espira.jpg|thumb|upright=0.5 |alt=Campo magnético produzido por uma espira circular onde passa corrente |Campo magnético produzido por uma espira circular onde passa corrente]] | ||
| + | |||
A passagem da ''corrente eléctrica estacionária'' (i.e. cuja intensidade não varia no tempo) por um condutor cria um campo magnético \(\mathbf{B}\) além de produzir calor por efeito de Joule. As ''linhas de força magnética'' produzidas por um fio condutor linear são circulares e concêntricas com o condutor (ver figura). O módulo de \(B\)num ponto a uma distância \(r\)do fio (medida na perpendicular ao fio) é | A passagem da ''corrente eléctrica estacionária'' (i.e. cuja intensidade não varia no tempo) por um condutor cria um campo magnético \(\mathbf{B}\) além de produzir calor por efeito de Joule. As ''linhas de força magnética'' produzidas por um fio condutor linear são circulares e concêntricas com o condutor (ver figura). O módulo de \(B\)num ponto a uma distância \(r\)do fio (medida na perpendicular ao fio) é | ||
| Linha 163: | Linha 166: | ||
em que \(\mu_0 = 4 \pi× 10^{−7}\)H/m é a ''permeabilidade magnética'' do vazio. | em que \(\mu_0 = 4 \pi× 10^{−7}\)H/m é a ''permeabilidade magnética'' do vazio. | ||
| − | |||
| − | |||
| − | No caso de uma espira <ref>Termo que designa um circuito eléctrico fechado< | + | |
| + | No caso de uma espira <ref>Termo que designa um circuito eléctrico fechado</ref> circular, é criado um campo magnético cujas linhas de força são curvas fora do seu eixo e lineares apenas ao longo do eixo. Pode provar-se que o campo magnético criado por uma espira de raio \(r\) percorrida por uma corrente de intensidade \(I\) tem linhas de força fechadas <ref>Mesmo aquelas que só ''fecham'' no infinito</ref>, ao contrário das linhas de força eléctricas. Isto coloca em evidência que \(\mathbf{B}\) nos pontos do plano da espira, mas exteriores a esta, é antiparalelo a \(\mathbf{B}\) no eixo da espira (ver figura). O módulo de \(\mathbf{B}\) num ponto do eixo é dado por | ||
<math display=“block”> | <math display=“block”> | ||
Revisão das 15h56min de 27 de março de 2024
Determinação experimental da relação \(q/m\) do electrão
Objectivo do trabalho
Pretende-se com este trabalho determinar a relação entre a carga e a massa \(q/m\) do electrão. Para esse fim, vamos estudar a deflexão de um feixe de raios catódicos sob o efeito de um campo eléctrico e de um campo magnético.
Conceitos fundamentais
Os raios catódicos foram descobertos em 1879 por William Crookes (1832--1919), mas foi Sir J. J. Thomson\footnote{Prémio Nobel da Física de 1906, em reconhecimento dos seus trabalhos teóricos e experimentais na condução da electricidade em gases.} (1856--1940) que, em 1897, relatou as experiências por si realizadas e que permitiram determinar o valor daquela relação. Além disso, estas experiências provaram que os raios catódicos são constituídos por partículas de carga negativa, desde então designadas por electrões. Neste trabalho iremos reproduzir aproximadamente a experiência de Thomson.
[math] h \nu _0 = e \phi \quad ou \quad \nu _0 = \frac{e}{h} \phi [/math]
[math] {\mathbf E(r,z)} = E_0 \, \hat{\mathbf x} \, \frac{w_0}{w(z)} \exp \left( \frac{-r^2}{w(z)^2}\right ) \exp \left(\! -i \left(kz +k \frac{r^2}{2R(z)} - \psi(z) \right) \!\right) [/math]
Os raios catódicos foram descobertos em 1879 por William Crookes (1832--1919), mas foi Sir J. J. Thomson\footnote{Prémio Nobel da Física de 1906, em reconhecimento dos seus trabalhos teóricos e experimentais na condução da electricidade em gases.} (1856--1940) que, em 1897, relatou as experiências por si realizadas e que permitiram determinar o valor daquela relação. Além disso, estas experiências provaram que os raios catódicos são constituídos por partículas de carga negativa, desde então designadas por electrões. Neste trabalho iremos reproduzir aproximadamente a experiência de Thomson.
Campo electrostático
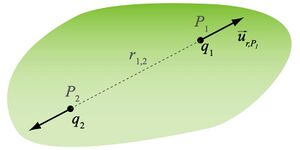
Define-se como sendo o campo eléctrico criado por uma distribuição de cargas que não evolui no tempo. Considere-se por exemplo o par de cargas \(q_1\)e \(q_2\) imersas no vácuo, à distância \(r_{12}\) e situadas respetivamente em \(P_1\)e \(P_2\) conforme ilustrado na figura à direita. A força eléctrica que sofre \(q_1\)no ponto \(P_1\)devido a \(q_2\)em \(P_2\)à distância \(r_{12}\)é
[math] \begin{equation} \mathbf{F}_{P_1,q_1} (q_2, r_{1 2} ) =\frac{1}{4 \pi \varepsilon_0}\frac{q_1 q_2}{r_{1 2}^2} \hat{\mathbf{u}}_{r,P_1} = - \mathbf{F}_{P_2,q_2} (q_1, r_{1 2} ) \label{eq:eq1} \end{equation} [/math]
em que \(\varepsilon_0\) é designada por constante dieléctrica ou permitividade eléctrica do vazio (\(\varepsilon_0 \simeq 8.854 \cdot 10^{-12}\)F/m) e \(\hat{\mathbf{u}}_{r,P_1}\) é o versor da distância \(r_{1 2}\) no ponto \(P_1\) (vector unitário dirigido de \(P_2\) para \(P_1\), ver figura).
Dada uma carga \(q_1\) e um ponto \(P\) a uma distância \(r\), define-se o campo eléctrico \(\mathbf{E}\) em \(P\)como a força eléctrica por unidade de carga exercida sobre uma carga de prova ou teste, suposta unitária e positiva, colocada em \(P\):
[math] \mathbf{E}_P (q_1, r) = \frac{q_1}{4 \pi \varepsilon_0 r^2} \hat{\mathbf{u}}_{r, P} [/math]
As unidades do campo eléctrico são o newton/coulomb (N/C) ou, mais habitualmente, o volt/metro (V/m).
As linhas de força eléctrica geradas por \(q_1\)são radiais e dirigidas para o exterior, se \(q_1>0\) ou para a origem, se \(q_1<0\). Se se colocasse em \(P\) a carga \(q\), a força eléctrica a que esta carga ficaria submetida devido a \(q_1\) seria \(\mathbf{F}_{P,q} (q_1, r ) = q \mathbf{E}\) ou mais simplesmente:
[math] \mathbf{F} = q \mathbf{E} [/math]
A expressão campo eléctrico também define a região do espaço onde se fazem sentir as acções eléctricas.
Potencial eléctrico
O campo eléctrico e a força eléctrica, que são entidades vectoriais, podem também ser calculadas a partir de uma função capaz de descrever o campo mas de natureza escalar, o potencial eléctrico \(V\). Para a situação referida acima, o potencial eléctrico criado no ponto \(P\) à distância \(r\) da carga \(q_1\) é calculado por:
[math] \label{eq:pot_ele} V_P (q_1, r) = \frac{q_1}{4 \pi \varepsilon_0 r} [/math]
No caso de uma distribuição de \(n\) cargas eléctricas \(q_i\) à distância \(r_i\) do ponto \(P\) onde se pretende calcular o campo eléctrico e o potencial, tem-se para o campo eléctrico
[math] \mathbf{E}_P = \frac{1}{4 \pi \varepsilon_0 } \sum_{i=1}^n \Big( \frac{q_i}{ r_i^2}\; \hat{\mathbf{u}}_{r_i , P} \Big) [/math]
e para o potencial
[math] V_P = \frac{1}{4 \pi \varepsilon_0 } \sum_{i=1}^n \Big( \frac{q_i}{ r_i} \Big) \nonumber [/math]
Recorde-se que se se considera uma única carga \(q_1\) positiva, as linhas de força eléctricas são radiais e dirigidas para o exterior. Essas linhas de força são perpendiculares às superfícies equipotenciais, que são esféricas \((r = \mathrm{c.^{te}})\) na equação \ref{eq:pot_ele}) e concêntricas com as cargas. Atendendo a (\ref{eq:pot_ele}) para dois raios \(r_1\) e \(r_2\) tal que \(r_2 > r_1\) temos \(V(r_2) < V(r_1)\) e portanto as linhas de força dirigem-se para os potenciais decrescentes.
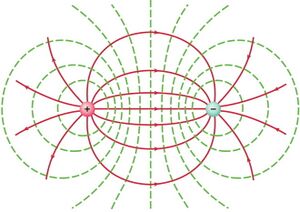
Considere-se agora o caso de duas cargas \(q_1 > 0\) e \(q_2 < 0\). Enquanto estiverem muito afastadas uma da outra, produzem campos radiais, respetivamente divergindo e convergindo. Se forem colocadas suficientemente próximas, as linhas de força vão sofrer a influência de ambas as cargas. Nesse caso, apenas uma única linha de força é linear, dirigida de \(q_1\) para \(q_2\). Todas as outras, que na vizinhança próxima de cada carga são radiais, acabam por infletir, dirigindo-se de \(q_1\) para \(q_2\). A figura das linhas de força tem simetria de revolução em torno do eixo que contém \(q_1\) e \(q_2\) e é esquematicamente a indicada na figura ao lado. Se o valor absoluto das duas cargas for o mesmo a figura é simétrica em relação ao plano mediatriz das cargas \(q_1\) e \(q_2\).[1]
Se se calcular a diferença de potencial entre dois pontos infinitamente próximos \(P\) e \(P+dP\) devida a uma carga \(q_1\) à distância \(r\) e \(r+dr\) respetivamente, a variação elementar do potencial \(V\) será:
[math] d V = V_{P+dP} - V_P = \frac{q_1}{4 \pi \varepsilon_0 r} \big( \frac{1}{r + dr} -\frac{1}{r} \big) \approx \frac{q_1}{4 \pi \varepsilon_0 } \big( - \frac{dr}{r^2} \big) = - \mathbf{E} \cdot d \mathbf{r} [/math]
Esta quantidade representa o trabalho elementar (energia) associado ao deslocamento da carga teste (\(q_t=1\,\)C), de \(P\) para \(P+dP\). Para \(q_1 > 0\) \(\mathbf{E}\) e \(\mathbf{dr}\) são paralelos e \(dV < 0\). Isto significa que não será necessário fornecer energia para realizar esse transporte.
De facto, afastar a carga teste da carga \(q_1\) (i.e. ir de \(P\) para \(P+dP\)) leva a uma configuração de cargas \(q_1\) e \(q_t\) energeticamente mais favorável.Erro de citação: Elemento de fecho </ref> em falta para o elemento <ref> circular, é criado um campo magnético cujas linhas de força são curvas fora do seu eixo e lineares apenas ao longo do eixo. Pode provar-se que o campo magnético criado por uma espira de raio \(r\) percorrida por uma corrente de intensidade \(I\) tem linhas de força fechadas [2], ao contrário das linhas de força eléctricas. Isto coloca em evidência que \(\mathbf{B}\) nos pontos do plano da espira, mas exteriores a esta, é antiparalelo a \(\mathbf{B}\) no eixo da espira (ver figura). O módulo de \(\mathbf{B}\) num ponto do eixo é dado por
[math] |\mathbf{B}_{\mathrm{espira}}| = \frac{\mu_0 I}{2 r} \sin^3 \alpha [/math]
Força de Lorentz
Uma carga q animada de uma velocidade\(\mathbf{v}\)numa região em que existe um campo de indução\(\mathbf{B}\)e um campo eléctrico\(\mathbf{E}\)fica submetida a uma força de Lorentz\footnote{Se a força for apenas de origem magnética,\(\mathbf{F}_m = q\,(\mathbf{v} \times \mathbf{B})\) pode chamar-se também de \emph{Laplace}}\(\mathbf{F}\)dada por: [math] \label{eq:Lorentz} \mathbf{F} = q\; \mathbf{E} + q\,(\mathbf{v} \times \mathbf{B}) [/math]
A força de Lorentz resulta da soma vectorial de uma componente eléctrica e uma componente magnética, que verificam as seguintes propriedades: \begin{itemize} \item a força eléctrica\(\mathbf{F_e}=q\mathbf{E}\)tem a mesma direção que o campo eléctrico; se a carga for positiva tem o mesmo sentido, se a carga for negativa tem o sentido oposto; \item a força magnética\(\mathbf{F_e}=q(\mathbf{v} \times \mathbf{B})\)é perpendicular ao plano definido pelos vectores velocidade\((\mathbf{v})\)e campo magnético\((\mathbf{B})\) sendo o seu sentido dado pela regra da mão direita para o produto externo de vectores. \end{itemize} Quando a velocidade da carga e o campo magnético são mutuamente perpendiculares, a força magnética comporta-se como uma força centrípeta e a carga descreve uma trajectória circular (ver Fig. \ref{fig:lorentz1}) cujo raio se pode calcular igualando os módulos das duas forças\((|\mathbf{F_c}|=|\mathbf{F_m})|$:
\begin{figure}[t]
\centering
\includegraphics[width=0.4\textwidth]{./Lorentz1.png} \caption{Trajectória circular para uma carga positiva\(q\)com velocidade\(\mathbf{v}\)na presença de um campo magnético\(\mathbf{B}_{in}\)perpendicular. \label{fig:lorentz1}} \end{figure}
\begin{figure}[h]
\centering
\includegraphics[width=0.5\textwidth]{./Lorentz2.png} \caption{ Carga positiva\(q\)com velocidade\(\mathbf{v}\) na presença de um campo magnético\(\mathbf{B}_{in}\)e um campo eléctrico\(\mathbf{E}$. Os três vectores são mutuamente perpendiculares e estão orientados de modo que as forças têm sentidos opostos. \label{fig:lorentz2}} \end{figure}
[math] m\frac{v^2}{R}=qvB \rightarrow R=\frac{mv}{|q|B} [/math]
Um caso particularmente interessante da força de Lorentz verifica-se quando a velocidade da carga é perpendicular tanto ao campo eléctrico como ao magnético. Nesse caso, as duas forças têm a mesma direcção. Adotando uma configuração como a representada na Fig. \ref{fig:lorentz2}, as forças eléctrica e magnética têm sentidos opostos e podem compensar-se, anulando-se, o que permite que a carga mantenha uma trajectória rectilínea.
Nesta repetição da experiência de Thomson iremos utilizar estes dois princípios para determinar a razão\(q/m$. Num primeiro conjunto de medidas, iremos determinar o raio da trajectória de um feixe de raios catódicos na presença de um campo magnético. No segundo conjunto de medidas iremos equilibrar as forças de um campo magnético e um eléctrico de modo a que o feixe tenha uma forma aproximadamente rectilínea.
\newpage
Figuras dos aparelhos da montagem experimental
\begin{figure}[ht] \centering \includegraphics[width=0.45\textwidth]{./fig3-ThomsomEquip} \caption{Montagem da Experiência de Thomson com tubo de raios catódicos, suporte e par de bobinas de Helmholtz. \label{fig:Thomson_Equip}} \end{figure}
\begin{figure}[hb] \centering \includegraphics[width=0.4\textwidth]{./fig4-Thomson_Electron-Deflection-Tube-D} \caption{Trajectória dos electrões sujeitos a um campo magnético perpendicular. \label{fig:Thomson_trajec}} \end{figure}
\newpage
Procedimento Experimental
Material
- Ampola (tubo) de raios catódicos (TRC), modelo TEL 525.
- Fonte de alimentação do TRC, que inclui alimentação de alta tensão contínua (até 5000 V) aplicada aos eléctrodos (cátodo e ânodo) do TRC e alimentação de baixa tensão (6.3 V AC) para o filamento do TRC.
- Par de bobinas que envolvem a parte esférica do TRC na configuração de Helmholtz (para criar um campo magnético aproximadamente homogéneo na região central entre as bobinas, de raio médio\(r\) e afastadas de\(r\)uma da outra).
- Fonte de alimentação de corrente \textbf{contínua} (em modo DC) para as bobinas.
- Multímetro (como amperímetro) a instalar em \textbf{série} no circuito das bobinas.
O tubo TRC tem um filamento alimentado por 6.3 V (em modo AC). Este filamento emite electrões por efeito termiónico. Entre o ânodo e o cátodo do tubo estabelecem-se diferenças de potencial\( (V_+ - V_-) = U_a\). Os electrões são acelerados entre o cátodo e o ânodo e a sua velocidade à saída do ânodo é função de\(U_a$.
Ao entrarem na parte esférica do tubo, os electrões podem ser deflectidos por \emph{campos magnéticos} provocados por correntes que percorrem as bobinas de Helmholtz e/ou por \emph{campos eléctricos} devidos à aplicação de tensão entre duas placas paralelas ligadas aos pontos 1 e 2 do diagrama (Fig. \ref{fig:TL}).
O campo de indução magnética\(B\)devido às bobinas de Helmholtz é aproximadamente uniforme na região central entre as bobinas, e para uma corrente\(I\)é dado por\footnote{No sistema SI, a unidade de campo magnético é o Tesla (T), sendo 1\,T=1\,Weber/m$^{2}\).}: \begin{align} \label{eq:helmotz} n &= 320\textrm{ espiras} \nonumber \\ B = \left(\frac{4}{5}\right)^{3/2} \cdot \frac{\mu_0 n I}{r} = \frac{32 \pi n }{5 \sqrt{5}} \cdot \frac{I}{r} \cdot 10^{-7}\textrm{ Weber/m}^{2}
\qquad r &= 0.068\textrm{ m} \\
r &= d/2 \nonumber \end{align}
\begin{figure} [h] \centering \includegraphics[width=1\textwidth]{fig5-TuboTL.pdf} \caption{Diagrama do tubo utilizado e geometria das bobinas de Helmholtz. Esquerda: vista lateral, com ligações eléctricas do filamento e da tensão de aceleração. Direita: vista frontal, com ligações das bobinas de Helmholtz. \label{fig:TL}} \end{figure}
Determinação de \(q/m\) por deflexão magnética
Trajectórias de partículas carregadas sujeitas a um campo magnético constante
Quando se aplica uma tensão\(U_a\)entre o ânodo e o cátodo (sem aplicar tensão entre os pontos 1 e 2 representados na Fig. \ref{fig:TL}), pode admitir-se que a velocidade final\(v\)dos electrões ao abandonarem o ânodo é dada pela seguinte expressão
[math] \label{eq:encin11} q\, U_a = \frac{1}{2} m \, v^2 [/math] em que\(q\) é a carga do electrão e\(m\)a sua massa.
Os electrões entram, com velocidade horizontal, na parte esférica do tubo, onde são deflectidos pelo campo magnético\(\vec{B}\)(com\(\vec{B}\perp\vec{v})$. A sua trajectória passa então a ser circular, com raio\(R\) verificando-se: [math] \label{eq:encin12} B \, q\, v = \frac{m\,v^2}{R} [/math]
As trajectórias dos electrões podem ser visualizadas numa escala graduada feita de material fluorescente. A origem do reticulado está situada aproximadamente no início da zona sujeita ao campo \(\mathbf{B}\). Combinando (\ref{eq:encin11}) e (\ref{eq:encin12}) obtém-se uma expressão para a relação\(q/m$: \begin{equation} \label{eq:encin3}
\frac{q}{m} = \frac{2\, U_a}{B^2\,R^2}
\end{equation} em que: \begin{description} \item[$U_a$] – impõe-se e mede-se diretamente no voltímetro da fonte de tensão. \item[$B$] – calcula-se, para uma dada corrente\(I\) a partir da expressão (\ref{eq:helmotz}). \item[$R$] – determina-se por leitura no écran fluorescente, das coordenadas de posição\(y\)(horizontal) e\(z\)(vertical) de pontos do feixe. Por construção do tubo verifica-se: \begin{equation} \label{eq:eR}
R = \frac{y^2 + z^2}{2 \, z}
\end{equation} \end{description}
Modo de proceder
\begin{enumerate} \item Montar os circuitos eléctricos de acordo com a Fig. \ref{fig:TL}. Note que as ligações das bobinas devem garantir que a corrente eléctrica é percorrida no mesmo sentido, em ambas: para isso, deve usar os conectores na ordem\(A\rightarrow Z\)numa bobina e na ordem inversa na outra bobina. Chamar o docente para verificação, \textbf{antes de ligar os aparelhos}. \item Verfifique qual é o valor máximo da tensão disponível na fonte de alta tensão. Escolha um valor ligeiramente inferior. \item Ajustar a corrente das bobinas de Helmholtz\(I_+\)de modo a que a circunferência passe por um ponto bem determinado\footnote{Utilize de preferência os maiores valores possíveis para o raio\(R\) de forma a que o feixe se encontre na zona central entre as bobines.}. Calcule\(R$. Inverta o sentido da corrente e determine um novo\(I_-\)para o mesmo raio\(R$. Tomando\(I_{\textrm{medio}} = (I_+ + I_-)/2\( calcule o campo magnético\(B_{\textrm{medio}}$. Utilize a semi-diferença,\((I_+ - I_-)/2\) para a estimativa das incertezas\(\delta I_{\textrm{medio}}\)e\(\delta B_{\textrm{medio}}$. \item Repita o ponto 2) para quatro novos valores de\(R$. \item Repetir 1), 2) e 3) e para os mesmos\(R\) para dois valores inferiores de tensão, afastados por exemplo de 500 V entre si. \item Apresente os valores de\(q/m\)para os 15 pares de determinações. Calcule a média desses valores, assim como a incerteza da média. \item Para um dos pares de pontos, estime a contribuição relativa das incertezas das grandezas que mediu para a incerteza total. Compare este erro assim calculado com a incerteza calculada a partir dos 15 valores calculados. Apresente para cada raio o valor de\(q/m\)assim como o erro associado a cada uma das determinações. Compare e comente os resultados. \item Apresente um valor final para\(q/m$. Estime a precisão e a exatidão obtida nas determinações que realizou. \end{enumerate}
Determinação de \(q/m\) por deflexão magnética e eléctrica quase compensada
Situação de equilíbrio entre as interacções eléctrica e magnética
Se, na força de Lorentz, os dois termos se equilibrarem -- ou seja, se as forças electrostática e magnética forem de igual módulo e de sentidos opostos -- a carga\(q\)não é desviada da sua trajectória. No nosso caso, em que\(\vec{B} \perp \vec{v}\), a condição de equilíbrio é dada por: \begin{equation} \label{eq:equil1}
|\vec{E}| = v\, |\vec{B}|
\end{equation}
Montagem a efectuar
Aproveitando a montagem já efectuada no ponto anterior, ligue agora os terminais 1 e 2 (Fig. \ref{fig:TLE}) à fonte de alta tensão que gera a tensão\(U_a\) produzindo assim na região do écran fluorescente um campo eléctrico. Fazendo com que as bobinas sejam percorridas por uma corrente com intensidade e ``sentido convenientes, podemos obter uma força de origem magnética anti-paralela à provocada pelo campo\(\vec{E}$. Deste modo, a trajectória visualizada no écran será aproximadamente retilínea, sendo a condição de equilíbrio dada por:
\begin{equation} \label{eq:equil2}
|\vec{E}| = v\, |\vec{B}| = \frac{U_a}{d}
\end{equation} onde\(d\)é a distância entre as placas do écran fluorescente e\(U_a\)a tensão entre as mesmas, que é como se disse igual à tensão de aceleração.
\begin{figure} [h] \centering \includegraphics[width=1\textwidth]{fig6-TuboTLE.pdf} \caption{Deflexão magnética e eléctrica quase compensada: ligações eléctricas do filamento, da tensão de aceleração e das placas. \label{fig:TLE}} \end{figure}
A equação (\ref{eq:equil2}) permite-nos calcular a velocidade dos electrões, uma vez que podemos conhecer os valores de todas as outras variáveis aí intervenientes. O conhecimento de\(v\)permite-nos calcular\(q/m\)tendo em conta que, segundo (\ref{eq:encin11}), deverá ser:
\begin{equation*} \label{eq:encin1} \frac{q}{m} = \frac{v^2}{2} \; \frac{1}{U_a} \end{equation*}
Ou finalmente, por combinação com (\ref{eq:equil2}): \begin{equation} \label{eq:qmquase} \frac{q}{m} = \frac{1}{2} \; \frac{U_a}{B^2\; d^2} \end{equation}
Modo de proceder
\begin{enumerate} \item Para cada uma das quatro tensões de trabalho\(U_a\)já referidas, aplicadas agora também às placas que produzem o campo eléctrico, determine o valor de\(B\)(a partir de\(I$) que conduz ao anulamento das forças de origem eléctrica e magnética. \item Inverta o sentido dos campos eléctricos e magnéticos e repita a determinação do valor de\(B$. \item Apresente os valores de\(q/m$. Analise as diferentes contribuições para a incerteza total. Estime o valor da relação carga/massa do electrão, assim como a precisão e a exatidão obtida nas determinações que realizou. \item Observe a trajectória quando as forças de origem eléctrica e magnética não se compensam. Comente. % Apresente os valores de q/m calculados assim como o erro associado a cada determinação. Apresente um valor final para\(q/m$. \end{enumerate}
- ↑ Para mais exemplos ver https://phet.colorado.edu/en/simulations/charges-and-fields
- ↑ Mesmo aquelas que só fecham no infinito