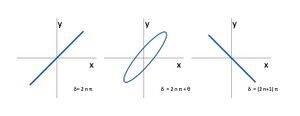Velocidade da luz

Determinação para diferentes materiais homogéneos e isotrópicos

Objectivo do trabalho

• Medição da velocidade da luz em diferentes meios homogéneos e isotrópicos: ar, vidro acrílico, água.
• Medição do índice de refracção dos mesmos materiais.

Conceitos fundamentais

Fig.1 - Esquema do aparelho (Roda de Fizeau) para determinar a velocidade da luz utilizado por Fizeau em 1849.

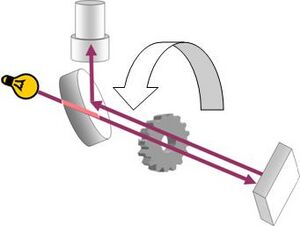
Em muitas das experiências descritas na literatura para determinacão da velocidade da luz foram utilizados feixes luminosos pulsados (ou modulados), que percorrem determinados trajetos de maior ou menor comprimento (ver exemplo na Fig. 1). No presente trabalho, utiliza-se como fonte luminosa um díodo (LED) que emite radiação visível com um comprimento de onda (c.d.o.) na zona do vermelho. A tensão de alimentação do díodo é sinusoidal de frequência$f_{\textrm{mod}}=50$ MHz, fazendo com que a intensidade da luz emitida $I_{\textrm{diodo}}(t)$seja modulada em amplitude (AM, do inglês amplitude modulation), variando entre 0 e $I_0$ de acordo com a expressão

$$\label{eq:f_am} I_{\textrm{diodo}}(t) = \frac{1}{2}I_0 [1+ \sin ( 2\pi f_{\textrm{mod}} t)]$$

Introdução

Base do método

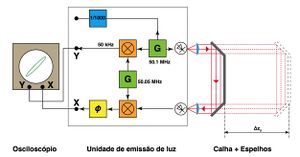
No presente trabalho, o feixe luminoso proveniente do LED emissor é forçado a percorrer um determinado trajeto de comprimento $L$, sendo em seguida a sua intensidade detectada por um fotodíodo receptor (Fig. 2). Um par de espelhos colocados a 90$^\circ$pode deslocar-se ao longo de uma calha, sendo assim possível variar o comprimento do trajeto. Os sinais de amplitude impostos ao emissor e captados no receptor são registados nos canais de um osciloscópio funcionando em modo “XY” (sem base de tempo).

Fig.2 - Montagem para determinação da velocidade da luz

Em ambos os canais X e Y (vertical e horizontal) a frequência é a mesma. No caso mais geral em que os sinais não estão em fase um com o outro, o padrão visualizado no osciloscópio é uma \emph{figura de Lissajous}, neste caso uma elipse (Fig. $\ref{fig:fase}$), com um parâmetro$\delta$dado pela equação geral:

$$\label{eq:elipse} \sin^2 \delta = \frac{A_x^2}{A_{x0}^2} + \frac{A_y^2}{A_{y0}^2} - \frac{2 A_y\,A_x}{A_{y0}\,A_{x0}} \cos \delta$$ sendo$A_x(t)$o sinal de intensidade captado no emissor, $A_y(t)$o sinal proveniente do recetor,$A_{x0}$,\(A_{y0}$as respectivas amplitudes e$\delta$a desfasagem entre os dois sinais. A desfasagem relativa entre os sinais (e, logo, o ângulo$\delta$) varia com o comprimento do trajecto\(L$percorrido pelo raio luminoso. Este efeito traduz-se numa variação da forma da elipse observada. A elipse pode degenerar em retas quando os dois sinais estiverem em fase,$\delta = 2n\pi$(nos quadrantes ímpares) ou em oposição de fase,$\delta = (2n+1)\,\pi$(nos quadrantes pares).

Figuras de Lissajous observadas no osciloscópio. À esquerda: sinais em fase; centro: sinais com uma dada desfasagem\(\theta$; direita: sinais em oposição de fase.

Velocidade da luz no ar

Neste trabalho, a velocidade da luz é calculada a partir da determinação do comprimento do caminho suplementar$\Delta L= 2\,\Delta z_0$(ver Fig. $\ref{fig:Montagem}$) que a luz tem de percorrer para que se passe de um extremo em que os sinais estão em fase ao extremo oposto de oposição de fase (ou vice-versa). Por definição, para passar de uma situação à outra é necessário que o tempo gasto no percurso suplementar corresponda a metade de um período. Assim, a luz percorre essa distância num intervalo de tempo$\Delta t$igual a metade do período do sinal modulante, ou seja\(\Delta t=T/2=1/(2\cdot50\,\textrm{MHz})= 10\,\textrm{ns}$. No trajecto da luz no ar teremos a seguinte expressão para a sua velocidade:

$$\label{eq:vc} c_{ar} = \frac{\Delta L}{\Delta t}=\frac{2\,\Delta z_0}{T/2}$$

Velocidade da luz em meios sólidos e líquidos

O índice de refração de um meio material\(1\)em relação a outro meio\(0$, para um dado comprimento de onda, é definido\footnote{Esta definição só é válida se as condutividades eléctricas dos meios\(0\)e\(1\)forem nulas, ou seja, nos \emph{dieléctricos} perfeitos.}
como o quociente entre as velocidades de propagação da luz nos meios\(0\)e\(1$:

[math]
	\label{eq:index}
	n_1 \equiv \frac{c_0}{c_1}  = \frac{\frac{1}{\sqrt{\varepsilon_0 \, \mu_0}} }{\frac{1}{\sqrt{\varepsilon_1 \, \mu_1}} } =
		\sqrt{\frac{\varepsilon_1 \, \mu_1}{\varepsilon_0 \, \mu_0}} = \sqrt{\varepsilon_r \, \mu_r}
[/math]

Nesta expressão$\varepsilon_0$,\(\varepsilon_1$, $\mu_0$,\(\mu_1$são as constantes dieléctricas e as permeabilidades magnéticas respetivamente do meios$0$e$1$e$\varepsilon_r$,\(\mu_r$ as relativas\((\varepsilon_1= \varepsilon_r\, \varepsilon_0)$.

Montagem para determinar índices de refração em sólidos e líquidos.

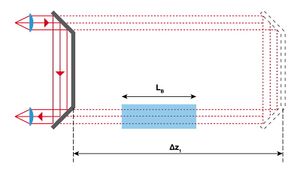
Se no percurso do feixe luminoso interpusermos um bloco transparente de material sólido ou líquido de comprimento$l_B$(Fig. $\ref{fig:Montagem_bloco}$), o comprimento suplementar necessário$\Delta L$entre as posições de fase e oposição de fase vai variar. De facto, uma vez que as velocidades da luz nesse material e no ar são diferentes, a desfasagem introduzida por uma dada espessura de material também difere da desfasagem causada pela mesma espessura de ar. É pois necessário contabilizar em separado os tempos necessários para percorrer

1. o bloco de espessura$l_B$à velocidade\(c_B$
2. o restante comprimento$(2\Delta z_1-l_B)$no ar à velocidade\(c_{ar}$

Obtém-se assim a expressão

$$\label{eq:vc_bloco} {T/2} = \frac{2\,\Delta z_1 - l_B}{c_{ar}} + \frac{l_B}{c_{B}}$$ em que$\Delta z_1$é a nova posição em que se regista passagem de fase para oposição de fase (ou vice-versa). A partir daqui calcula-se a velocidade\(c_{B}$.

Pode ainda obter-se o valor do índice de refração$n_{B}$com a ajuda de ($\ref{eq:vc}$) e ($\ref{eq:index}$):

$$\begin{align} \label{eq:n_bloco} {T/2} = \frac{2\,\Delta z_0}{c_{ar}} &= \frac{2\,\Delta z_1 }{c_{ar}} - \frac{l_B}{c_{ar}} + \frac{l_B}{c_{B}} \nonumber \\ \frac{2\,(\Delta z_0- \Delta z_1 )}{c_{ar}} &= - \frac{l_B}{c_{ar}} + \frac{l_B}{c_{B}} \nonumber \\ \frac{2\,(\Delta z_0- \Delta z_1 )}{l_B} &= -1 + \frac{c_{ar}}{c_{B}} \nonumber \\ n_{B} &= 1 + \frac{2\,(\Delta z_0- \Delta z_1 )}{l_B} \end{align}$$

Neste trabalho, serão determinados os índices de refração e a velocidade da luz em dois meios materiais: a resina acrílica e a água.

Procedimento experimental

Material

1. Unidade de emissão (com amplitude modulada por um sinal de frequência 50 MHz) e de recepção de luz.

% (díodos receptor) amplitude modulada por um sinal de frequência\(50\,MHz$)(.

1. Duas lentes plano-esféricas em suportes de tipo poste, ajustáveis
2. Suporte móvel com dois espelhos planos para inversão do sentido de propagação da luz.
3. Calha de aço inox.
4. Banco óptico de altura ajustável.
5. Bloco de vidro acrílico transparente.
6. Dois tubos com cerca de 1 metro de comprimento para conter água ou ar.
7. Osciloscópio de dois canais a funcionar em modo XY.

\end{enumerate}

Trabalho preparatório

\begin{enumerate}

1. Preencha os objectivos do trabalho que irá realizar na sessão de laboratório.
2. Preencha o quadro com as equações necessárias para o cálculo das grandezas, bem como as suas incertezas.

\end{enumerate}

Regulação da montagem

Posicionamento das lentes no suporte da unidade de emissão de luz.

1. Comece por efectuar o alinhamento óptico do sistema. Ligue a unidade e posicione a lente junto ao LED emissor. Usando um alvo difusor (papel vegetal, por exemplo), observe a forma da mancha luminosa ao longo do percurso óptico, Ajuste a lente de modo a obter um diâmetro constante (feixe de raios paralelos, ou colimado) e à mesma altura relativamente à mesa. Note que pode ajustar a altura da lente, a sua posição transversal e a distância ao LED.
2. Instale o conjunto de espelhos, assegurando-se de que o feixe incide em ambas as superfícies espelhadas (se for necessário, ajuste de novo a primeira lente, mas sem perder a forma do feixe que obteve). O suporte e os espelhos estão pré-alinhados, pelo que não deverá necessitar de ajustar os seus suportes. Verifique que os espelhos enviam o feixe de volta correctamente. Ainda sem a segunda lente, verifique que a mancha luminosa está centrada com a janela do díodo receptor. Se não estiver, ajuste a primeira lente (e não os espelhos).
3. Coloque agora a lente no lado do díodo receptor e, ajustando-a, alinhe o foco do feixe convergente de modo a incidir no centro do díodo (ver figura $\ref{fig:lentes}$).
4. Ligue o osciloscópio às saídas da unidade emissora e visualize ambos os canais (modo DUAL). Optimize a posição da lente no díodo receptor de modo a maximizar a amplitude do \emph{sinal recebido}. Quando tiver terminado, volte a colocar o osciloscópio em mode XY e ajuste de modo a visualizar uma figura de Lissajous contida no écran.
5. Coloque os espelhos na posição zero (posição\(z_{\delta=0}$) da escala -- por exemplo, encostando o suporte dos espelhos ao suporte da unidade emissora. Rodando o botão da unidade que ajusta electronicamente a diferença de fase entre os dois sinais, obtenha uma reta dos quadrantes (ím)pares.

Montagem para medição da velocidade da luz no ar.

Medição da velocidade de propagação da luz no ar

1. Desloque os espelhos sobre a calha e observe a modificação da figura no ecrã do

osciloscópio, em particular nas posições que correspondem a que os sinais recebidos estejam em quadratura$(\delta=\pi/2)$e oposição de fase$(\delta=\pi)$. Para esta última situação, registe a nova posição\(z_{\delta=\pi}$dos espelhos e o intervalo de incerteza entre o qual os sinais parecem estar ainda em oposição de fase (ver figura $\ref{fig:ar}$).

1. Repita o procedimento para cada observador.
2. Calcule a velocidade de propagação da luz no ar$c_{ar}$, a sua incerteza e o desvio à exatidão\footnote{O valor\(c_{ar}$é muito próximo de$c_{vacuo}$= 299 792 458 m/s, que é uma constante exacta do Sistema Internacional de Medidas. O índice de refração do ar para a luz visível é\(n_{ar}=1.000293$.}.

Montagem para medição da velocidade da luz no vidro acrílico.

Medição da velocidade de propagação da luz no vidro acrílico

1. Verifique novamente se no zero da posição dos espelhos os sinais estão em fase. Usando o banco óptico, ajuste a altura e coloque cuidadosamente o bloco de vidro acrílico no percurso do feixe incidente, de modo a que incida perpendicularmente à face e usando o percurso mais longo no vidro acrílico (figura $\ref{fig:vidro}$)
2. Meça a posição$z_{\delta=\pi}$e a incerteza correspondente dos espelhos para que os dois sinais detetados estejam em oposição em fase.
3. Repita a medição pelo menos duas vezes.
4. Calcule o índice de refração obtido para o vidro acrílico,\(n_{vidro}$, pela expressão (\ref{eq:n_bloco}), e a sua incerteza.
5. Calcule o valor da velocidade da luz no vidro,\(c_{vidro}$.

thumb|upright=1.0 |alt= Montagem para medição da velocidade da luz na água.| Montagem para medição da velocidade da luz na água.

Medição da velocidade de propagação da luz na água

1. Verifique a fase na posição inicial. Com o auxílio do banco óptico e dos dois suportes (ver figura $\ref{fig:agua}$), coloque cuidadosamente o tubo \emph{vazio} de modo a que o feixe incidente entre perpendicularmente à face. Pode desmontar este tubo para medir o comprimento interno do trajeto no ar/água.
2. Registe a posição dos espelhos$z_{\delta=\pi}^{\textup{tubo}}$que produz um sinal em oposição de fase.
3. Repita a medição para o tubo \emph{cheio de água} e obtenha o valor correspondente\(z_{\delta=\pi}^{\textup{água}}$.
4. Calcule o valor do índice de refração$n_{\textup{água}}$obtido, a sua incerteza e o desvio à exatidão\footnote{O valor tabelado é\(n_{\textup{água}}=1.3330$.}.
5. Comente a precisão do valor da velocidade de propagação da luz obtida nos

diferentes meios.

Análise, conclusões e comentários finais

Discuta a qualidade dos dados obtidos e as conclusões que pode retirar desta experiência. Comente também sobre as condições de realização da experiência, dos equipamentos utilizados e a influência de erros aleatórios e sistemáticos, identificando-os.