Diferenças entre edições de "Experiência de Millikan"
| (Há 43 edições intermédias do mesmo utilizador que não estão a ser apresentadas) | |||
| Linha 1: | Linha 1: | ||
| − | + | <big>Estimativa da carga eléctrica de gotículas de óleo electrizadas em suspensão num fluido</big> | |
| + | |||
| + | {|class="wikitable" style="background-color:#ccddff;" | ||
| + | | Não consegue ver as equações correctamente? Mude https para http no endereço desta página e recarregue. | ||
| + | |} | ||
=Objectivo do trabalho= | =Objectivo do trabalho= | ||
| − | Pretende-se com este trabalho determinar a | + | [[File:MI-RAMillikan.jpeg|thumb|upright=0.5|Robert A. Millikan]] |
| + | Pretende-se com este trabalho determinar a [https://pt.wikipedia.org/wiki/Carga_el%C3%A9trica carga eléctrica] de pequenas gotas de óleo, tendo como objetivo final mostrar que a carga eléctrica não aparece com uma quantidade qualquer mas sempre como um múltiplo de uma unidade fundamental: a [https://pt.wikipedia.org/wiki/Carga_do_el%C3%A9tron carga do electrão]. Deste modo, um corpo electrizado apresenta um excesso de carga de sinal positivo ou negativo, mas cuja valor é sempre um múltiplo do valor da carga elementar | ||
| + | {| border="0" cellpadding="5" cellspacing="0" align="center" | ||
| + | ! style="background:#ddffdd;" |\(q_{ele}= -1,602176634\cdot 10^{-19}\) \(\mathrm{C}\). | ||
| + | |} | ||
| − | + | Traduz-se este facto dizendo-se que a carga eléctrica é ''quantizada''. | |
| − | |||
| − | + | Dentro das várias experiências elaboradas para mostrar este facto, uma montagem clássica é a do físico americano [https://pt.wikipedia.org/wiki/Robert_Andrews_Millikan Robert A. Millikan] (1869-1953), que recebeu o prémio Nobel da Física em 1923 pelos seus trabalhos sobre a determinação da carga do electrão e [https://pt.wikipedia.org/wiki/Efeito_fotoel%C3%A9trico efeito fotoeléctrico]. Esta experiência é também chamada [https://pt.wikipedia.org/wiki/Experi%C3%AAncia_da_gota_de_%C3%B3leo experiência da gota de óleo]. O método usado na experiência pode ser resumido nos seguintes passos: | |
| + | * Estudar a queda de pequenas gotículas de óleo electrizadas sob acção simultânea da gravidade e de um campo eléctrico uniforme | ||
| + | * Determinar a força de gravidade (calcular a velocidade limite) | ||
| + | * Determinar a força eléctrica (cancelar com força de gravidade) | ||
| − | + | =Conceitos fundamentais= | |
| + | ==Corpo esférico em queda livre num fluido== | ||
| + | [[file:MI-gotas-chuva.png|thumb|upright=1.0 |alt=Gotas de chuva. |As gotas de chuva em queda livre adquirem naturalmente uma forma esférica.]] | ||
| + | [[file:millikan-graph.png|thumb|upright=1.0 |alt=Evolução da velocidade de um corpo em queda livre sujeito a uma força de atrito. |Fig. 1 - Evolução da velocidade de um corpo em queda livre sujeito a uma força de atrito.]] | ||
| + | Um corpo de dimensões muito pequenas<ref>Com [https://pt.wikipedia.org/wiki/Coeficiente_de_Reynolds número de Reynolds] \(Re= \frac{\rho v L}{\eta}\) inferior a \(\simeq 100\)</ref>, ao mover-se com uma velocidade relativamente baixa através de um fluido (líquido ou gás), fica sujeito a uma [https://pt.wikipedia.org/wiki/Atrito força de atrito] aproximadamente proporcional à sua velocidade, modelada pela expressão: | ||
| − | + | {| border="0" cellpadding="5" cellspacing="0" align="center" | |
| + | ! style="background:#efefef;" |<math>\mathbf{F}_{at} = - k \, \eta \mathbf{v}</math>|| \(\quad\quad (1)\) | ||
| + | |} | ||
| − | + | em que \(\eta\) é o coeficiente de [https://pt.wikipedia.org/wiki/Viscosidade viscosidade] do fluido, \(\mathbf{v}\) é a velocidade do corpo e \(k\) é um coeficiente que depende da forma do corpo, que no caso deste ser uma esfera de raio \(R\) toma o valor ([https://pt.wikipedia.org/wiki/Lei_de_Stokes lei de Stokes]): | |
| − | \ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| border="0" cellpadding="5" cellspacing="0" align="center" | |
| + | ! style="background:#efefef;" |<math> k = 6 \pi R</math>|| \(\quad\quad (2)\) | ||
| + | |} | ||
| − | + | O coeficiente \(k\) virá assim expresso em ''metro'' no Sistema Internacional (SI) e o coeficiente de viscosidade em Pa\(\cdot\)s (ou N\(\cdot\)s/m\(^2\)). | |
| + | Normalmente a unidade de viscosidade que aparece na literatura é a unidade do sistema C.G.S. (g/cm\(\cdot\)s) que é designada por Poise (abreviatura P), verificando-se então a equivalência: | ||
| − | + | {| border="0" cellpadding="5" cellspacing="0" align="center" | |
| − | + | ! style="background:#efefef;" |<math>1 \, \mathrm{P} = 0,1\, \mathrm{Pa}\cdot\mathrm{s}</math> | |
| − | </math> | + | |} |
| − | + | Quando um corpo de massa \(m\) cai em queda livre sob a ação do seu peso \(\mathbf{P}=m\mathbf{g}\) através de um fluido, o seu movimento de queda será abrandado pela força de atrito, e a equação do movimento escreve-se<ref>Uma vez que o movimento de queda ocorre unicamente ao longo do eixo vertical, podemos implicitamente passar da descrição vectorial para uma escalar.</ref>: | |
| − | + | {| border="0" cellpadding="5" cellspacing="0" align="center" | |
| − | + | ! style="background:#efefef;" |<math>ma \equiv m\frac{dv}{dt} = mg - k\eta v</math>|| \(\quad\quad (3)\) | |
| + | |} | ||
| − | + | A partir de uma velocidade inicial nula, e sendo o peso do corpo constante, a aceleração \(a\) produz um aumento em \(v(t)\) e, por consequência, um aumento na força de atrito \(F_{at}\). Para uma determinada velocidade limite \(v_L\), o segundo membro de (3) anula-se e o corpo passará a deslocar-se com movimento uniforme. A [https://pt.wikipedia.org/wiki/Velocidade_terminal velocidade limite] \(v_L\) será então obtida fazendo \(a= 0\) na equação (3): | |
| − | \ | ||
| − | |||
| − | |||
| − | == | + | {| border="0" cellpadding="5" cellspacing="0" align="center" |
| − | + | ! style="background:#efefef;" |<math>v_L = \frac{m\,g}{k \, \eta}</math>|| \(\quad\quad (4)\) | |
| − | + | |} | |
| − | < | + | o que poderá ser facilmente constatado pela resolução <ref>Ver notas de apoio às aulas teóricas.</ref> da equação (3), cuja solução é da forma: |
| − | |||
| − | </ | ||
| − | + | {| border="0" cellpadding="5" cellspacing="0" align="center" | |
| + | ! style="background:#efefef;" |<math>v(t) = \frac{m\,g}{k \, \eta} (1 - e^{- (k\,\eta / m) t}) = v_L (1-e^{-t/\tau})</math>|| \(\quad\quad (5)\) | ||
| + | |} | ||
| − | + | à qual corresponde o gráfico da Fig. 1, e onde se definiu o tempo característico \(\tau=k\eta/m\). Quando \(t \to \infty\) temos \(v(t) \to v_L = \frac{mg}{k \eta}\). | |
| − | \ | ||
| − | |||
| − | e para o | + | ==Impulsão e peso aparente== |
| + | [[file:MI-Archimedes-principle.png|thumb|upright=1 |alt=Princípio de Arquimedes. |Fig. 2 - Princípio de Arquimedes.]] | ||
| + | Se pretendermos ser mais rigorosos, devemos substituir em (4) o peso do corpo pelo seu''peso aparente'' no fluido. De facto, um corpo em queda livre através de um fluido experimenta, além da ação da força de atrito, outra força de baixo para cima cujo módulo é igual ao peso do fluido deslocado pelo corpo, de acordo com o [https://pt.wikipedia.org/wiki/Impuls%C3%A3o Princípio de Arquimedes]. A Fig. 2 ilustra este princípio: uma massa \(m=\)5 kg mergulhada em água desloca \(m_a=\)2 kg de água, pelo que o seu peso aparente é \(P=(m-m_a)g\). | ||
| − | + | Assim, as equações (3) e (4) deverão ser modificadas para: | |
| − | |||
| − | |||
| − | + | {| border="0" cellpadding="5" cellspacing="0" align="center" | |
| + | ! style="background:#efefef;" |<math>m\,a = m\,g - m_f\,g - k \, \eta \, v</math>|| \(\quad\quad (6)\) | ||
| + | |} | ||
| − | + | {| border="0" cellpadding="5" cellspacing="0" align="center" | |
| + | ! style="background:#efefef;" |<math>v_L = \frac{(m - m_f)\,g}{k \, \eta}</math>|| \(\quad\quad (7)\) | ||
| + | |} | ||
| − | + | onde \(m_f\)é a massa do fluido deslocado. No caso de um corpo esférico de raio \(R\), introduzindo a equação (2) em (7) e atendendo a que: | |
| − | + | {| border="0" cellpadding="5" cellspacing="0" align="center" | |
| + | ! style="background:#efefef;" |<math>m = \frac{4}{3} \pi R^3 \rho \quad \textrm{ e } \quad m_f = \frac{4}{3} \pi R^3 \rho_f</math> | ||
| + | |} | ||
| − | + | obtemos a expressão corrigida para a velocidade limite | |
| − | |||
| − | |||
| − | + | {| border="0" cellpadding="5" cellspacing="0" align="center" | |
| − | + | ! style="background:#efefef;" |<math>v_L = \frac{2\,R^2\, (\rho - \rho_f)\,g}{9 \, \eta}</math>|| \(\quad\quad (8)\) | |
| + | |} | ||
| − | + | em que \(\rho\) e \(\rho_f\)são as massas específicas do corpo e do fluido. Note-se que conhecendo o raio do corpo é pois possível determinar a sua velocidade limite de queda, e vice-versa. | |
| − | + | ==Equilíbrio dum corpo carregado, imerso num fluido, através de um campo eléctrico vertical== | |
| − | + | [[file:f_equil.jpg|thumb|upright=1.0 |alt=Equilíbrio de forças numa gota sujeita a campos gravítico e eléctrico. |Fig. 3 - Equilíbrio de forças numa gota sujeita a campos gravítico e eléctrico.]] | |
| − | + | Considere o esquema representado na Fig. 3, em que um fluido não condutor se encontra entre duas placas condutoras paralelas separadas de uma distância \(d\). Ao aplicar-se uma diferença de potencial \(U = V_1 -V_2 > 0\) com a polaridade indicada na figura, é criado um campo eléctrico ascendente. Se entre as placas se encontrar uma partícula de massa \(m\)e carga positiva <ref>No caso da partícula estar carregada negativamente obteríamos o mesmo resultado invertendo o sentido do campo eléctrico.</ref> \(q\) esta ficará sujeita a uma força eléctrica que contrariará a sua queda. | |
| + | Na hipótese do campo eléctrico ser uniforme <ref>Nomeadamente, se a distância entre as placas for muito menor que as suas dimensões laterais.</ref> o módulo de \(\mathbf{E}\)e o módulo da força eléctrica \(\mathbf{F}_e\) que atua na partícula serão dados por: | ||
| − | + | {| border="0" cellpadding="5" cellspacing="0" align="center" | |
| − | + | ! style="background:#efefef;" |<math>E = \frac{U}{d}, \qquad F_e = |q| \frac{U}{d}</math> | |
| − | + | |} | |
| − | e | + | Assim, a queda da partícula será agora contrariada pela força eléctrica e pela força de atrito. |
| + | A equação (6) passa a escrever-se: | ||
| − | + | {| border="0" cellpadding="5" cellspacing="0" align="center" | |
| − | + | ! style="background:#efefef;" |<math>m\,a = (m - m_f)\,g - q \frac{U}{d} - k \, \eta_{ar} \, v</math>|| \(\quad\quad (9)\) | |
| − | + | |} | |
| − | + | Variando a diferença de potencial (ddp) \(U\), pode-se estabelecer o equilíbrio entre o peso da partícula e a força eléctrica, conseguindo-se a sua paragem entre as placas. Nessa situação, tem-se simultaneamente \(F_{at}=0\), \(a=0\) e \(v\) \(=0\): | |
| − | <math | + | {| border="0" cellpadding="5" cellspacing="0" align="center" |
| − | + | ! style="background:#efefef;" |<math>0 = (m - m_f)\,g - q \frac{U}{d}</math>|| \(\quad\quad (10)\) | |
| − | </math> | + | |} |
| − | + | Nesta equação a expressão \((m - m_f)\,g\) pode ser substituída usando a equação (7), obtendo-se: | |
| − | |||
| − | {| | + | {| border="0" cellpadding="5" cellspacing="0" align="center" |
| − | | | + | ! style="background:#efefef;" |<math>v_L\, k\, \eta_{ar} = q \frac{U}{d}</math> |
| − | |||
|} | |} | ||
| − | + | E entrando também com a eq. (2) no caso de a partícula ser esférica, obtemos por fim: | |
| − | + | {| border="0" cellpadding="5" cellspacing="0" align="center" | |
| − | + | ! style="background:#efefef;" |<math>q = \frac{6 \pi \, R \, \eta_{ar} \, d\, v_L}{U}</math>|| \(\quad\quad (11)\) | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | <math | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | onde entram as seguintes grandezas | |
{| class="wikitable" | {| class="wikitable" | ||
| − | |||
|- | |- | ||
| − | | | + | ! Símbolo !! Valor !! Descrição |
| + | |- | ||
| + | | \(v_L\) || A medir || Velocidade limite de queda da partícula através do fluido, na ausência de campo eléctrico | ||
| + | |- | ||
| + | | \(\eta_{ar}\) || 18,52\(\cdot\)10\(^{-5}\) P =18,52\(\cdot\)10\(^{-6}\) Pa\(\cdot\)s || Viscosidade do ar a 23\(^{\circ}\) C | ||
| + | |- | ||
| + | | \(\rho\) || 973 kg/m\(^{3}\) || Massa específica do óleo de silicone | ||
| + | |- | ||
| + | | \(\rho_f\) || 1 kg/m\(^{3}\) || Massa específica do ar | ||
| + | |- | ||
| + | | \(g\) || 9,80 m/s\(^{2}\) || Aceleração gravítica em Lisboa | ||
|- | |- | ||
| − | | | + | | \(d\) || A medir || Distância entre placas |
|} | |} | ||
| − | = | + | ==Correções== |
| − | == | + | ===Temperatura ambiente=== |
| − | + | No caso da temperatura ambiente se afastar muito de 23\(^{\circ}\) C, o valor da viscosidade do ar terá de ser corrigido.<ref>Utilize por exemplo a calculadora ''online'': http://www.lmnoeng.com/Flow/GasViscosity.htm</ref> | |
| − | + | ===Dimensão das gotas=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | A Lei de Stokes não é exata quando as dimensões dos corpos esféricos forem comparáveis à distância média entre as moléculas do ar. Nestas condições, Millikan verificou que a viscosidade \(\eta_{ar}\)deveria ser substituída por: | |
| − | |||
| − | + | {| border="0" cellpadding="5" cellspacing="0" align="center" | |
| + | ! style="background:#efefef;" |<math>\eta_{ar}' = \frac{\eta_{ar}}{1 + b/(p\,R)}</math>|| \(\quad\quad (12)\) | ||
| + | |} | ||
| − | + | em que a constante \(b=7,88\cdot 10^{-3}\) Pa\(\cdot\)m, \(p\) é pressão atmosférica expressa em pascal e \(R\) é o raio da gota em metros. O valor corrigido \(q'\) será determinado a partir do valor experimental \(q\) por | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| border="0" cellpadding="5" cellspacing="0" align="center" | |
| + | ! style="background:#efefef;" |<math>q' = q\, \left(\frac{\eta_{ar}'}{\eta_{ar}}\right)^{3/2} =q\, \left(\frac{1}{1 + b/(p\,R)}\right)^{3/2}</math>|| \(\quad\quad (13)\) | ||
| + | |} | ||
| − | = | + | =Figuras dos aparelhos da montagem experimental= |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{| class="wikitable" | {| class="wikitable" | ||
| + | |+ Vista do aparelho de Millikan | ||
| + | |- | ||
| + | | [[file:U131001_01_Aparelho-de-Millikan.jpg|thumb|upright=1.0 |alt=Equipamento para determinação da carga das gotas.]] || [[file:U13105-230_01_Aparelho-operacional-de-Millikan.jpg|thumb|upright=1.0 |alt=Gerador de alta tensão DC regulável.]] | ||
|- | |- | ||
| − | | | + | | Fig. 4 - Equipamento para determinação da carga das gotas. || Fig. 5 - Gerador de alta tensão DC regulável. |
| − | |||
| − | |||
|} | |} | ||
| + | =Procedimento experimental= | ||
| − | + | ==Material== | |
| − | |||
| − | |||
| − | |||
| − | + | * Célula de Millikan com gerador de alta tensão DC regulável | |
| − | + | * Atomizador e óleo de silicone | |
| + | * Cronómetro | ||
| + | * Nível de bolha de ar | ||
| − | === | + | {|class="wikitable" style="background-color:#ffcccc;" |
| + | | [[file:Electrocution-Safety.png|thumb|upright=0.5]] || '''Atenção:''' Este trabalho envolve o uso de fontes de alta tensão (até 500 V DC). Assegure-se de que cumpre rigorosamente as medidas de segurança com equipamentos eléctricos, em particular: | ||
| + | * Compreenda os [https://pt.wikipedia.org/wiki/Choque_el%C3%A9trico riscos inerentes] a tensões e correntes elevadas | ||
| + | * Não pegue nos cabos ou conectores pela partes condutoras, apenas pelas partes isoladas | ||
| + | * Assegure-se de que as fontes de tensão e corrente estão dsligadas antes de efectuar qualquer alteração nas montagens eléctricas | ||
| + | * Em caso de dúvida, chame o docente | ||
| + | |} | ||
| − | # | + | ==Trabalho preparatório== |
| − | # | + | # Preencha os objectivos do trabalho que irá realizar na sessão de laboratório. |
| − | + | # Preencha o quadro com as equações necessárias para o cálculo das grandezas, bem como as suas incertezas. | |
| − | + | # Desenhe um diagrama das forças a que uma gota está sujeita durante a experiência. Após a experiência, acrescente uma estimativa dos valores dessas forças usando valores típicos obtidos durante a experiência, e anexe tudo ao relatório final. | |
| − | |||
| − | |||
| − | # | ||
| − | |||
| − | == | + | ==Montagem experimental== |
| + | Efectue a montagem de acordo com a Fig. 6. Chame o professor antes de ligar os aparelhos à corrente eléctrica. | ||
| − | + | [[file:Esquema-Millikan.jpg|thumb|Fig. 6 - Esquema da montagem da experiência de Millikan. 1 - Célula de Millikan; 2 - lâmpada; 3 - gerador de alta tensão regulável; 4 - cronómetro.]] | |
| − | + | ==Determinação da tensão de equilíbrio== | |
| − | + | # Depois de verificar que a célula está horizontal, meça o distância entre placas, \(d\). Tente focar o microscópio na zona onde as gotas irão "flutuar". Atenção: o microscópio amplia a imagem e a escala por 2\(\times\). | |
| − | + | # Coloque o potenciómetro que controla a alimentação das placas do condensador no valor mínimo de tensão eléctrica. | |
| − | + | # Verifique se o interruptor de inversão da alimentação do condensador está na posição "Neutra". Rode o potenciómetro para uma posição que permita, quando ligar o interruptor de inversão, estabelecer um campo eléctrico entre as placas do condensador. | |
| − | + | # Utilizando o pulverizador junto do orifício da célula, produza uma pequena "nuvem" de gotículas de óleo. Observe através do microscópio o movimento das gotículas em frente do retículo, ajustando a focagem se necessário. | |
| − | + | # Ligando o interruptor e variando a intensidade e o sentido do campo eléctrico, verifique se existem gotículas eletrizadas. | |
| − | + | # Escolha uma das gotas e, ajustando a tensão, manipule a sua posição vertical de modo a que esta fique colocada numa determinada divisão do topo do retículo, imobilizando-a de seguida. Registe o valor da tensão. | |
| − | + | ==Determinação da velocidade limite e da carga== | |
| − | < | + | <ol> |
| − | + | <li value="7"> Anule o campo eléctrico e verifique que a gota cai sob acção da gravidade (com velocidade limite). | |
| − | + | Com um cronómetro, meça o tempo necessário para que a gota percorra \(N>4\) divisões do retículo. </li> | |
| − | + | <li> Repondo o campo eléctrico, conduza a gota para a posição inicial para medir o tempo pelo menos duas vezes.</li> | |
| − | + | <li> Troque de posição com o colega para repetir este processo para várias gotas, tentando escolher as gotas de menor carga.</li> | |
| − | + | <li> Para cada gota, calcule a velocidade limite média e a respectiva incerteza, usando esse valor para estimar o raio e a carga. Calcule a carga corrigida pela viscosidade.</li> | |
| − | + | <li> De modo a obter resultados mais fiáveis, tente assegurar-se de que as diversas gotas apresentam valores experimentais diferentes. Duas gotas com valores da velocidade limite e raio muito semelhantes têm provavelmente a mesma carga, pelo que deverá repetir as medições para uma gota diferente.</li> | |
| − | < | + | <li> Considere a expressão acima (Eq. 11) para a carga da gota e pondere quais as características ideais para obter resultados significativos, isto é, que contribuam para os objectivos da experiência. As gotas deverão ter \(R\) grande ou pequeno? A velocidade-limite deve ser grande ou pequena? E a tensão aplicada? Use estes critérios para decidir se vale a pena completar as medições para uma dada gota, após as medições preliminares. |
| − | + | </ol> | |
| − | </ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | ==Análise, conclusões e comentários finais== |
| + | Discuta a qualidade dos dados obtidos e as conclusões que pode retirar desta experiência. Comente também sobre as condições de realização da experiência, dos equipamentos utilizados e a influência de erros aleatórios e sistemáticos, identificando-os. Supondo que não conhecia o valor tabelado da carga do electrão, e apenas a partir dos resultados obtidos, poderá tirar conclusões sobre a quantificação da carga eléctrica? | ||
| − | + | =Notas= | |
| − | + | <references /> | |
| − | |||
| − | |||
| − | = | + | =Ligações externas= |
| + | * [https://www.youtube.com/watch?v=tPeXBrzsnxg The Millikan Experiment] Visualização das gotas de óleo numa experiência de Millikan | ||
| + | * [https://www.youtube.com/watch?v=nwnjYERS66U Millikan Oil Drop Experiment Animation] Animação da experiência de Thomson | ||
Edição atual desde as 15h09min de 10 de março de 2025
Estimativa da carga eléctrica de gotículas de óleo electrizadas em suspensão num fluido
| Não consegue ver as equações correctamente? Mude https para http no endereço desta página e recarregue. |
Objectivo do trabalho
Pretende-se com este trabalho determinar a carga eléctrica de pequenas gotas de óleo, tendo como objetivo final mostrar que a carga eléctrica não aparece com uma quantidade qualquer mas sempre como um múltiplo de uma unidade fundamental: a carga do electrão. Deste modo, um corpo electrizado apresenta um excesso de carga de sinal positivo ou negativo, mas cuja valor é sempre um múltiplo do valor da carga elementar
| \(q_{ele}= -1,602176634\cdot 10^{-19}\) \(\mathrm{C}\). |
|---|
Traduz-se este facto dizendo-se que a carga eléctrica é quantizada.
Dentro das várias experiências elaboradas para mostrar este facto, uma montagem clássica é a do físico americano Robert A. Millikan (1869-1953), que recebeu o prémio Nobel da Física em 1923 pelos seus trabalhos sobre a determinação da carga do electrão e efeito fotoeléctrico. Esta experiência é também chamada experiência da gota de óleo. O método usado na experiência pode ser resumido nos seguintes passos:
- Estudar a queda de pequenas gotículas de óleo electrizadas sob acção simultânea da gravidade e de um campo eléctrico uniforme
- Determinar a força de gravidade (calcular a velocidade limite)
- Determinar a força eléctrica (cancelar com força de gravidade)
Conceitos fundamentais
Corpo esférico em queda livre num fluido
Um corpo de dimensões muito pequenas[1], ao mover-se com uma velocidade relativamente baixa através de um fluido (líquido ou gás), fica sujeito a uma força de atrito aproximadamente proporcional à sua velocidade, modelada pela expressão:
| [math]\mathbf{F}_{at} = - k \, \eta \mathbf{v}[/math] | \(\quad\quad (1)\) |
|---|
em que \(\eta\) é o coeficiente de viscosidade do fluido, \(\mathbf{v}\) é a velocidade do corpo e \(k\) é um coeficiente que depende da forma do corpo, que no caso deste ser uma esfera de raio \(R\) toma o valor (lei de Stokes):
| [math] k = 6 \pi R[/math] | \(\quad\quad (2)\) |
|---|
O coeficiente \(k\) virá assim expresso em metro no Sistema Internacional (SI) e o coeficiente de viscosidade em Pa\(\cdot\)s (ou N\(\cdot\)s/m\(^2\)). Normalmente a unidade de viscosidade que aparece na literatura é a unidade do sistema C.G.S. (g/cm\(\cdot\)s) que é designada por Poise (abreviatura P), verificando-se então a equivalência:
| [math]1 \, \mathrm{P} = 0,1\, \mathrm{Pa}\cdot\mathrm{s}[/math] |
|---|
Quando um corpo de massa \(m\) cai em queda livre sob a ação do seu peso \(\mathbf{P}=m\mathbf{g}\) através de um fluido, o seu movimento de queda será abrandado pela força de atrito, e a equação do movimento escreve-se[2]:
| [math]ma \equiv m\frac{dv}{dt} = mg - k\eta v[/math] | \(\quad\quad (3)\) |
|---|
A partir de uma velocidade inicial nula, e sendo o peso do corpo constante, a aceleração \(a\) produz um aumento em \(v(t)\) e, por consequência, um aumento na força de atrito \(F_{at}\). Para uma determinada velocidade limite \(v_L\), o segundo membro de (3) anula-se e o corpo passará a deslocar-se com movimento uniforme. A velocidade limite \(v_L\) será então obtida fazendo \(a= 0\) na equação (3):
| [math]v_L = \frac{m\,g}{k \, \eta}[/math] | \(\quad\quad (4)\) |
|---|
o que poderá ser facilmente constatado pela resolução [3] da equação (3), cuja solução é da forma:
| [math]v(t) = \frac{m\,g}{k \, \eta} (1 - e^{- (k\,\eta / m) t}) = v_L (1-e^{-t/\tau})[/math] | \(\quad\quad (5)\) |
|---|
à qual corresponde o gráfico da Fig. 1, e onde se definiu o tempo característico \(\tau=k\eta/m\). Quando \(t \to \infty\) temos \(v(t) \to v_L = \frac{mg}{k \eta}\).
Impulsão e peso aparente
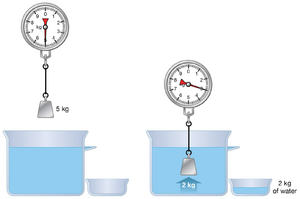
Se pretendermos ser mais rigorosos, devemos substituir em (4) o peso do corpo pelo seupeso aparente no fluido. De facto, um corpo em queda livre através de um fluido experimenta, além da ação da força de atrito, outra força de baixo para cima cujo módulo é igual ao peso do fluido deslocado pelo corpo, de acordo com o Princípio de Arquimedes. A Fig. 2 ilustra este princípio: uma massa \(m=\)5 kg mergulhada em água desloca \(m_a=\)2 kg de água, pelo que o seu peso aparente é \(P=(m-m_a)g\).
Assim, as equações (3) e (4) deverão ser modificadas para:
| [math]m\,a = m\,g - m_f\,g - k \, \eta \, v[/math] | \(\quad\quad (6)\) |
|---|
| [math]v_L = \frac{(m - m_f)\,g}{k \, \eta}[/math] | \(\quad\quad (7)\) |
|---|
onde \(m_f\)é a massa do fluido deslocado. No caso de um corpo esférico de raio \(R\), introduzindo a equação (2) em (7) e atendendo a que:
| [math]m = \frac{4}{3} \pi R^3 \rho \quad \textrm{ e } \quad m_f = \frac{4}{3} \pi R^3 \rho_f[/math] |
|---|
obtemos a expressão corrigida para a velocidade limite
| [math]v_L = \frac{2\,R^2\, (\rho - \rho_f)\,g}{9 \, \eta}[/math] | \(\quad\quad (8)\) |
|---|
em que \(\rho\) e \(\rho_f\)são as massas específicas do corpo e do fluido. Note-se que conhecendo o raio do corpo é pois possível determinar a sua velocidade limite de queda, e vice-versa.
Equilíbrio dum corpo carregado, imerso num fluido, através de um campo eléctrico vertical
Considere o esquema representado na Fig. 3, em que um fluido não condutor se encontra entre duas placas condutoras paralelas separadas de uma distância \(d\). Ao aplicar-se uma diferença de potencial \(U = V_1 -V_2 > 0\) com a polaridade indicada na figura, é criado um campo eléctrico ascendente. Se entre as placas se encontrar uma partícula de massa \(m\)e carga positiva [4] \(q\) esta ficará sujeita a uma força eléctrica que contrariará a sua queda. Na hipótese do campo eléctrico ser uniforme [5] o módulo de \(\mathbf{E}\)e o módulo da força eléctrica \(\mathbf{F}_e\) que atua na partícula serão dados por:
| [math]E = \frac{U}{d}, \qquad F_e = |q| \frac{U}{d}[/math] |
|---|
Assim, a queda da partícula será agora contrariada pela força eléctrica e pela força de atrito. A equação (6) passa a escrever-se:
| [math]m\,a = (m - m_f)\,g - q \frac{U}{d} - k \, \eta_{ar} \, v[/math] | \(\quad\quad (9)\) |
|---|
Variando a diferença de potencial (ddp) \(U\), pode-se estabelecer o equilíbrio entre o peso da partícula e a força eléctrica, conseguindo-se a sua paragem entre as placas. Nessa situação, tem-se simultaneamente \(F_{at}=0\), \(a=0\) e \(v\) \(=0\):
| [math]0 = (m - m_f)\,g - q \frac{U}{d}[/math] | \(\quad\quad (10)\) |
|---|
Nesta equação a expressão \((m - m_f)\,g\) pode ser substituída usando a equação (7), obtendo-se:
| [math]v_L\, k\, \eta_{ar} = q \frac{U}{d}[/math] |
|---|
E entrando também com a eq. (2) no caso de a partícula ser esférica, obtemos por fim:
| [math]q = \frac{6 \pi \, R \, \eta_{ar} \, d\, v_L}{U}[/math] | \(\quad\quad (11)\) |
|---|
onde entram as seguintes grandezas
| Símbolo | Valor | Descrição |
|---|---|---|
| \(v_L\) | A medir | Velocidade limite de queda da partícula através do fluido, na ausência de campo eléctrico |
| \(\eta_{ar}\) | 18,52\(\cdot\)10\(^{-5}\) P =18,52\(\cdot\)10\(^{-6}\) Pa\(\cdot\)s | Viscosidade do ar a 23\(^{\circ}\) C |
| \(\rho\) | 973 kg/m\(^{3}\) | Massa específica do óleo de silicone |
| \(\rho_f\) | 1 kg/m\(^{3}\) | Massa específica do ar |
| \(g\) | 9,80 m/s\(^{2}\) | Aceleração gravítica em Lisboa |
| \(d\) | A medir | Distância entre placas |
Correções
Temperatura ambiente
No caso da temperatura ambiente se afastar muito de 23\(^{\circ}\) C, o valor da viscosidade do ar terá de ser corrigido.[6]
Dimensão das gotas
A Lei de Stokes não é exata quando as dimensões dos corpos esféricos forem comparáveis à distância média entre as moléculas do ar. Nestas condições, Millikan verificou que a viscosidade \(\eta_{ar}\)deveria ser substituída por:
| [math]\eta_{ar}' = \frac{\eta_{ar}}{1 + b/(p\,R)}[/math] | \(\quad\quad (12)\) |
|---|
em que a constante \(b=7,88\cdot 10^{-3}\) Pa\(\cdot\)m, \(p\) é pressão atmosférica expressa em pascal e \(R\) é o raio da gota em metros. O valor corrigido \(q'\) será determinado a partir do valor experimental \(q\) por
| [math]q' = q\, \left(\frac{\eta_{ar}'}{\eta_{ar}}\right)^{3/2} =q\, \left(\frac{1}{1 + b/(p\,R)}\right)^{3/2}[/math] | \(\quad\quad (13)\) |
|---|
Figuras dos aparelhos da montagem experimental
| Fig. 4 - Equipamento para determinação da carga das gotas. | Fig. 5 - Gerador de alta tensão DC regulável. |
Procedimento experimental
Material
- Célula de Millikan com gerador de alta tensão DC regulável
- Atomizador e óleo de silicone
- Cronómetro
- Nível de bolha de ar
Atenção: Este trabalho envolve o uso de fontes de alta tensão (até 500 V DC). Assegure-se de que cumpre rigorosamente as medidas de segurança com equipamentos eléctricos, em particular:
|
Trabalho preparatório
- Preencha os objectivos do trabalho que irá realizar na sessão de laboratório.
- Preencha o quadro com as equações necessárias para o cálculo das grandezas, bem como as suas incertezas.
- Desenhe um diagrama das forças a que uma gota está sujeita durante a experiência. Após a experiência, acrescente uma estimativa dos valores dessas forças usando valores típicos obtidos durante a experiência, e anexe tudo ao relatório final.
Montagem experimental
Efectue a montagem de acordo com a Fig. 6. Chame o professor antes de ligar os aparelhos à corrente eléctrica.
Determinação da tensão de equilíbrio
- Depois de verificar que a célula está horizontal, meça o distância entre placas, \(d\). Tente focar o microscópio na zona onde as gotas irão "flutuar". Atenção: o microscópio amplia a imagem e a escala por 2\(\times\).
- Coloque o potenciómetro que controla a alimentação das placas do condensador no valor mínimo de tensão eléctrica.
- Verifique se o interruptor de inversão da alimentação do condensador está na posição "Neutra". Rode o potenciómetro para uma posição que permita, quando ligar o interruptor de inversão, estabelecer um campo eléctrico entre as placas do condensador.
- Utilizando o pulverizador junto do orifício da célula, produza uma pequena "nuvem" de gotículas de óleo. Observe através do microscópio o movimento das gotículas em frente do retículo, ajustando a focagem se necessário.
- Ligando o interruptor e variando a intensidade e o sentido do campo eléctrico, verifique se existem gotículas eletrizadas.
- Escolha uma das gotas e, ajustando a tensão, manipule a sua posição vertical de modo a que esta fique colocada numa determinada divisão do topo do retículo, imobilizando-a de seguida. Registe o valor da tensão.
Determinação da velocidade limite e da carga
- Anule o campo eléctrico e verifique que a gota cai sob acção da gravidade (com velocidade limite). Com um cronómetro, meça o tempo necessário para que a gota percorra \(N>4\) divisões do retículo.
- Repondo o campo eléctrico, conduza a gota para a posição inicial para medir o tempo pelo menos duas vezes.
- Troque de posição com o colega para repetir este processo para várias gotas, tentando escolher as gotas de menor carga.
- Para cada gota, calcule a velocidade limite média e a respectiva incerteza, usando esse valor para estimar o raio e a carga. Calcule a carga corrigida pela viscosidade.
- De modo a obter resultados mais fiáveis, tente assegurar-se de que as diversas gotas apresentam valores experimentais diferentes. Duas gotas com valores da velocidade limite e raio muito semelhantes têm provavelmente a mesma carga, pelo que deverá repetir as medições para uma gota diferente.
- Considere a expressão acima (Eq. 11) para a carga da gota e pondere quais as características ideais para obter resultados significativos, isto é, que contribuam para os objectivos da experiência. As gotas deverão ter \(R\) grande ou pequeno? A velocidade-limite deve ser grande ou pequena? E a tensão aplicada? Use estes critérios para decidir se vale a pena completar as medições para uma dada gota, após as medições preliminares.
Análise, conclusões e comentários finais
Discuta a qualidade dos dados obtidos e as conclusões que pode retirar desta experiência. Comente também sobre as condições de realização da experiência, dos equipamentos utilizados e a influência de erros aleatórios e sistemáticos, identificando-os. Supondo que não conhecia o valor tabelado da carga do electrão, e apenas a partir dos resultados obtidos, poderá tirar conclusões sobre a quantificação da carga eléctrica?
Notas
- ↑ Com número de Reynolds \(Re= \frac{\rho v L}{\eta}\) inferior a \(\simeq 100\)
- ↑ Uma vez que o movimento de queda ocorre unicamente ao longo do eixo vertical, podemos implicitamente passar da descrição vectorial para uma escalar.
- ↑ Ver notas de apoio às aulas teóricas.
- ↑ No caso da partícula estar carregada negativamente obteríamos o mesmo resultado invertendo o sentido do campo eléctrico.
- ↑ Nomeadamente, se a distância entre as placas for muito menor que as suas dimensões laterais.
- ↑ Utilize por exemplo a calculadora online: http://www.lmnoeng.com/Flow/GasViscosity.htm
Ligações externas
- The Millikan Experiment Visualização das gotas de óleo numa experiência de Millikan
- Millikan Oil Drop Experiment Animation Animação da experiência de Thomson