Equação do plano tangente

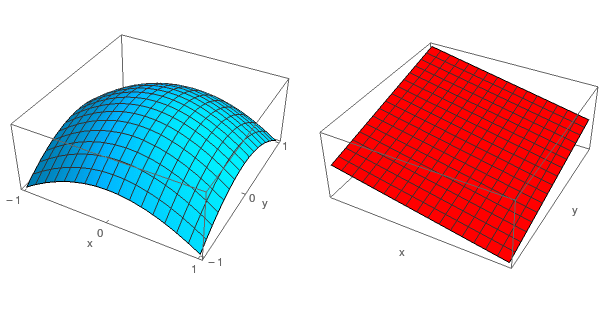
Na figura seguinte pode ver-se o gráfico da função \(f\)\(\left(\begin{array}{c}x\\y\\\end{array}\right)\)=\(e^{\sqrt{-x^2-y^2+9}}\) para \( -1 \leq x,y \leq 1 \) e o plano tangente ao gráfico da função no ponto correspondente a \(\left(\begin{array}{c}\frac{1}{2}\\-\frac{1}{2}\\\end{array}\right)\)

Uma equação cartesiana do plano tangente é dada por:

A) \(-\frac{e^{\sqrt{\frac{17}{2}}}\left(x-\frac{1}{2}\right)}{\sqrt{34}}+\frac{e^{\sqrt{\frac{17}{2}}}\left(y+\frac{1}{2}\right)}{\sqrt{34}}-z+e^{\sqrt{\frac{17}{2}}}\text{=0}\)

B) \(-\frac{e^{\sqrt{\frac{17}{2}}}\left(x-\frac{1}{2}\right)}{\sqrt{34}}+\frac{e^{\sqrt{\frac{17}{2}}}\left(y+\frac{1}{2}\right)}{\sqrt{34}}-z-e^{\sqrt{\frac{17}{2}}}\text{=0}\)

C) \(\frac{e^{\sqrt{\frac{17}{2}}}\left(x+\frac{1}{2}\right)}{\sqrt{34}}-\frac{e^{\sqrt{\frac{17}{2}}}\left(y-\frac{1}{2}\right)}{\sqrt{34}}-z+e^{\sqrt{\frac{17}{2}}}\text{=0}\)

D) \(\frac{e^{\sqrt{\frac{17}{2}}}(x-1)}{\sqrt{34}}-\frac{e^{\sqrt{\frac{17}{2}}}(y+1)}{\sqrt{34}}-z+e^{\sqrt{\frac{17}{2}}}\text{=0}\)

Para obter o zip que contém as instâncias deste exercício clique aqui[1]

Se deseja obter o código fonte que gera os exercícios contacte miguel.dziergwa@ist.utl.pt