Erros e incertezas experimentais

Não consegue ver as equações correctamente? Mude https para http no endereço desta página e recarregue.

Grandezas físicas

Um dos principais objectivos da Física Experimental consiste na medição quantitativa de grandezas físicas. A palavra medição designa o acto de medir, do qual resulta uma medida (ou mais do que uma, no caso de se repetir o processo). É fundamental classificar os principais tipos de grandezas encontradas:

Tipos de grandezas físicas

Directas	São aquelas cujo valor se obtém com uma medição, não sendo necessário envolver os valores de outras grandezas físicas. Exemplos: comprimento \(L\) tempo \(t\) temperatura \(T\) massa \(m\)
Indirectas	São aquelas que envolvem a medição de duas ou mais grandezas, que por sua vez podem ser directas (D) ou indirectas (I). Exemplos: velocidade (escalar) \(v\) - envolve comprimento (D) e tempo (D) área \(A\) - envolve comprimento (D) e largura (D) densidade \(\rho\) - envolve massa (D) e volume (I)
Escalares	São caracterizadas por um número e pela unidade de medida que a define. Exemplos: temperatura \(T\) (K) tempo \(t\) (s) massa \(m\) (kg)
Vectoriais	Além de um número e uma unidade de medida, é necessário também saber a direção e o sentido destas grandezas. Exemplos: posição espacial \(\vec{r}\) (m) velocidade \(\vec{v}\) (m/s) força \(\vec{F}\) (N)

Definições fundamentais

Precisão e exactidão

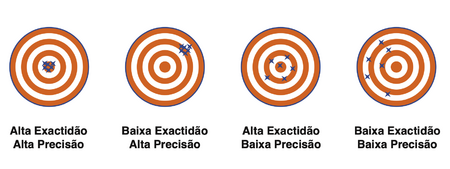
Na linguagem coloquial os termos precisão e exactidão usam-se como sinónimos, mas no método científico experimental traduzem conceitos muito diferentes. Pode existir uma medida exacta e não precisa, ou outra precisa mas não exacta (ver ilustração). O grande mérito de um experimentalista será obter simultaneamente a melhor precisão e a melhor exactidão possíveis.

A precisão de uma medição é o grau da concordância entre determinações repetidas: está relacionado com a variação das sucessivas medidas A exactidão é tanto maior quanto menor for a distância entre a medida (ou a média de determinações repetidas) e um valor “verdadeiro”, “nominal”, “tomado como referência” ou “aceite”. A esta distância damos o nome de erro experimental.

Numa actividade experimental, em regra geral, o valor verdadeiro das grandezas físicas não é conhecido a priori, pelo que naturalmente também não é possível calcular o valor do erro experimental. Nas actividades laboratoriais de LIFE existem algumas excepções em que este valor “verdadeiro/referência” é conhecido com grande precisão/exactidão (e.g Exp. Thomson, Exp. Millikan, Velocidade da Luz, etc). Outras há em que não se conhece o valor verdadeiro (e.g. carga de uma gota de óleo electrizada, temperatura da sala, índice de refração de um material transparente, etc).

Erros sistemáticos e aleatórios

Existem duas grandes contribuições para o erro experimental, uma de natureza sistemática e outra aleatória:

Erros sistemáticos

Erros aleatórios

Conduzem em geral a valores sistematicamente desviados (para valores superiores ou inferiores) do valor da grandeza a medir, contribuindo para uma menor exactidão. Podem ser originados por más condições de calibração dos instrumentos de medida o uso destes instrumentos em condições diferentes das que são recomendadas leituras sistematicamente incorrectas do observador (e.g. paralaxe) utilização de um método físico que não é adequado à descrição da experiência. Devem ser corrigidos e minimizados sempre que possível. Só a comparação dos resultados obtidos com outros instrumentos de referência (calibração) pode elucidar se esses erros foram suficientemente reduzidos.

Resultam das flutuações aleatórias que se observam nos resultados obtidos para diferentes leituras, contribuindo para uma menor precisão. Podem ser originados por falta de sensibilidade dos instrumentos e do observador leituras incorrectas (mas não sistemáticas) ruído (vibrações mecânicas ou eléctricas) processos estatísticos intrínsecos ao fenómeno observado (por exemplo declínio radioactivo). A análise estatística das flutuações está fora do âmbito da LIFE, mas importa referir que, habitualmente, considera-se o valor médio dos erros aleatórios como zero. Isto é importante pois, ao repetirem-se as medições e fazendo a média aos \(N\) resultados, os erros aleatórios compensam-se, reduzindo-se assim a contribuição aleatória. Os erros aleatórios podem e devem ser sempre caracterizados, mas dado o seu carácter estocástico, não podem ser eliminados totalmente, pelo que qualquer medição tem associada uma incerteza experimental.

Em conclusão, podemos resumir todos estes conceitos nestes pontos:

1. Toda a medição experimental é sujeita a um erro experimental. Só por grande coincidência o valor numérico obtido pela medição é igual ao valor verdadeiro da grandeza.
2. Antes da experiência, devemos identificar e corrigir os erros sistemáticos de todas as grandezas directas e das constantes utilizadas, de modo a minimizar os erros sistemáticos e aumentar a exactidão. No final, a comparação do valor médio obtido com o valor da mesma grandeza tabelado, nas mesmas condições físicas (ou proveniente de outras experiências), permite estimar o desvio à exactidão do valor obtido, que pode ser estimado em percentagem como

[math]\mathrm{desvio}(\%)=\left|\frac{\text { valor }_{\text {conhecido }}-\text { valor }_{\text {medido }}}{\text { valor }_{\text {conhecido }}}\right| \cdot 100[/math]

3. Porque existem sempre erros aleatórios, toda a medição é afectada de uma incerteza, que indica o grau de precisão. Obrigatoriamente em todos os resultados tem de se apresentar sempre o valor mais provável da grandeza, mais a respectiva estimativa numérica da incerteza. Exemplo: \(Vel_{som(ar)} =\) 343.5 ± 0.6 m/s
4. Quando se calculam grandezas indirectas a partir das medições directas, utilizando as equações físicas, as incertezas propagam-se, gerando uma incerteza do resultado final.

Veremos nas próximas secções como se pode, de uma forma simplificada, calcular e representar os valores mais prováveis para as grandezas directas e indirectas e as respectivas incertezas.

Resolução e sensibilidade

A resolução de um instrumento de medição é o menor intervalo mensurável com esse instrumento. É uma característica do seu desempenho em termos de qual o menor detalhe ou mudança que o instrumento consegue detectar. Por exemplo, na linguagem comum emprega-se o termo "resolução de um écran" para designar o nível de detalhe com que um aparelho reproduz imagens digitais. Em física experimental a resolução é estimada tendo em conta a menor escala ou algarismo exibido pelo instrumento e varia consoante este seja analógico ou digital:

Instrumentos analógicos	Considera-se que a resolução é metade da menor escala do instrumento. Exemplo: uma régua com divisões de 1 mm tem uma resolução de 0,5 mm, uma vez que a olho nu é possível perceber se uma dada medida está mais próxima de 9,5 mm ou de 10,0 mm.	A resolução desta escala analógica é 0,5 V.
Instrumentos digitais	Considera-se que a resolução corresponde à útima casa decimal exibida pelo instrumento, uma vez que essa é a incerteza sobre qual o arrendondamento que foi feito. Exemplo: Um voltímetro digital que mostre uma leitura de 12,6 V pode corresponder a um valor real contido entre 12,55 V e 12,65 V, pelo que a resolução é 0,1 V	A resolução desta escala digital é 0,1 V.

Por regra, a incerteza de uma medida (única) realizada com um instrumento é igual à sua resolução. No entanto, se a leitura do instrumento não permanecer constante – por exemplo, se a agulha de um voltímetro digital oscilar ou se os dígitos de um voltímetro digital variarem – a regra já não é válida e a incerteza deve ser estimada, usando bom senso, a partir do intervalo de variação.

A sensibilidade, por outro lado, é uma indicação do mínimo sinal detectável pelo instrumento, isto é, qual o valor mínimo que é necessário atingir para que uma leitura seja registada. Por exemplo, qual a menor massa que é necessário colocar no prato de uma balança para que esta registe o seu peso? Esse valor é a sua sensibilidade. Qual a menor divisão da escala da balança? Esse valor é a sua resolução.

Valor médio e incerteza nas medições experimentais

Grandezas directas

A repetição de uma medição da variável \(x\) nas mesmas condições experimentais conduz a uma distribuição aleatória de resultados em torno de um valor médio \(\bar{x}\) (média aritmética), que pode ser considerado como o melhor valor obtido nesta medida. Por exemplo, para \(N\) medidas \(x_1,x_2,...\) da grandeza \(x\) temos

[math]\bar{x}=\frac{x_1+x_2+...+x_N}{N}=\frac{\sum_i x_i}{N}[/math]	\(\quad\quad\) (Valor médio)

Num grande número de situações, esta repetição realizada \(N\) vezes nas mesmas condições experimentais conduz a um valor médio que se aproxima do “verdadeiro” valor da grandeza à medida que \(N\) aumenta. Devemos distinguir duas situações, dependendo do valor de \(N\):

\(N\) grande \((N\gg 10)\) Pode calcular-se o desvio padrão \(s\), que exprime a dispersão dos resultados: [math]s=\sqrt{\frac{\sum_i\left(x_i-\bar{x}\right)^2}{N-1}}[/math] \(\quad\quad\) (Desvio padrão) O melhor valor para a incerteza do valor médio \(u\), é dado pelo desvio padrão da média, \(u=s\sqrt{N}\), também chamado erro padrão ou erro padrão da média: [math]u=\sqrt{\frac{\sum_i\left(x_i-\bar{x}\right)^2}{N(N-1)}}[/math] \(\quad\quad\) (Incerteza do valor médio) O resultado final neste caso (para um número elevado de determinações nas mesmas condições experimentais) deve apresentar-se como: [math]\bar{x}\pm u[/math] \(\quad\quad\) (Apresentação de resultado final)

\(N\) pequeno \((1<N<10)\) Neste caso a análise estatística perde significado e a incerteza deve ser estimada usando um majorante \(\Delta x\), que será o maior desvio em relação ao valor médio: [math]\Delta x=\max|\bar{x}-x_i|[/math] Majorante dos desvios O resultado final neste caso pode apresentar-se numa das seguintes formas: [math]\bar{x}\pm\Delta x[/math] Resultado final, incerteza absoluta [math]\bar{x}\pm\Delta x/\bar{x}[/math] Resultado final, incerteza relativa No caso da incerteza relativa, o resultado é expresso em percentagem. Exemplo para \(\bar{x}=2\) e \(\Delta x=0.2\): [math] x=2.0\pm 0.2[/math] (incerteza absoluta) [math] x=2.0\pm 10\%[/math] (incerteza relativa) Importante: em qualquer caso, se a incerteza calculada for menor do que a incerteza intrínseca do instrumento (e.g. resolução da escala), a estimativa deve ser substituída por esta última.

Incerteza nas grandezas indirectas

Para uma grandeza indirecta \(F(X,Y,Z,…)\) sendo \(X,Y,Z,…\) grandezas medidas directas, com incertezas que foram estimadas pelas equações acima como sendo \(u_X , u_Y, u_Z\) pode estimar-se a incerteza \(u_F\) da grandeza \(F\) a partir das respectivas derivadas parciais:

[math]u_F=\sqrt{\left(\frac{\partial F}{\partial X} u_X\right)^2+\left(\frac{\partial F}{\partial Y} u_Y\right)^2+\left(\frac{\partial F}{\partial Z} u_X\right)^2 \cdots}[/math]

Quando não é possível fazer uma análise estatística \((1<N<4)\), um majorante do erro da grandeza indirecta \(\Delta F\) é calculável a partir de

[math]\Delta F=\left|\frac{\partial F}{\partial X}\right| \Delta X+\left|\frac{\partial F}{\partial Y}\right| \Delta Y+\left|\frac{\partial F}{\partial Z}\right| \Delta Z[/math]

onde \(\Delta X,\Delta Y,\Delta Z\), são as incertezas estimadas através dos majorantes dos erros das variáveis correspondentes. Caso estas incertezas sejam relevantes, as derivadas deverão ser calculadas por majoração.

Caso particular: para uma função racional (por ex. \(F(X,Y,Z)=cte∙X^a Y^b Z^c\), com \(a,b,c\) inteiros) o majorante do erro relativo pode ser dado simplesmente pela soma dos majorantes dos erros relativos das variáveis multiplicados pelos expoentes em valor absoluto:

[math]\Delta F/F=|a|\cdot\frac{\Delta X}{X}+|b|\cdot\frac{\Delta Y}{Y}+|c|\cdot\frac{\Delta Z}{Z}[/math]

Exemplo. Consideremos a velocidade escalar \(v=x/t\). É uma grandeza indirecta cujo medição envolve a medição das grandezas directas comprimento \(\bar{x}\pm\Delta x\) e tempo \(\bar{t}\pm\Delta t\). Para calcular a incerteza associada à velocidade, calculamos as respectivas derivadas parciais: [math]\left|\frac{\partial v}{\partial x}\right|=\frac{1}{t}\quad\quad\left|\frac{\partial v}{\partial t}\right|=\frac{x}{t^2} [/math] A majoração das derivadas faz-se calculando os seus valores na "pior" (maior valor numérico) situação, ou seja, maximizando os numeradores e minimizando os denominadores: [math]\left|\frac{\partial v}{\partial x}\right|_\mathrm{maj}=\frac{1}{t-\Delta t}\quad\quad\left|\frac{\partial v}{\partial t}\right|_\mathrm{maj}=\frac{x+\Delta x}{(t-\Delta t)^2} [/math] Para um número pequeno de medições obtemos a expressão para a incerteza do valor médio, [math]\Delta v=\frac{1}{t-\Delta t} \Delta x+\frac{x+\Delta x}{(t-\Delta t)^2} \Delta t[/math] Usando o "método expresso" do caso particular, uma vez que \(v=x^1t^{-1}\) podemos escrever [math]\frac{\Delta v}{v}=\frac{\Delta x}{x}+\frac{\Delta t}{t}\rightarrow\Delta v=\frac{\Delta x}{t}+\frac{x\Delta t}{t^2} [/math] Majorando os quocientes, voltamos a obter a expressão calculada explicitamente pelas derivadas parciais. Assim, este método é muito mais prático e rápido.

Representação de resultados da medição de grandezas

Regras fundamentais:

• Os resultados das medições devem ser apresentados com uma incerteza que, em regra geral, deve ter apenas um ou dois algarismos significativos
• Por sua vez, o valor mais provável deve usar as mesmas casas decimais, arredondando-se o algarismo mais à direita.
• Nunca esquecer também as unidades físicas da grandeza medida, de preferência no Sistema Internacional de Unidades.

Bons exemplos	\(R = 0.185\pm 0.030\, \mathrm{m}\) \(Temp = 297.0\pm 0.5\,\mathrm{K}\) \(v = 344.3\pm 0.4 \,\mathrm{m\cdot s}^{-1}\) \(B = (5.92\pm 0.08)\times10^{-4}\,\mathrm{ T}\) \(q/m = (1.77\pm 0.07)\times10^{11}\,\mathrm{ C\cdot kg}^{-1}\) \(e = 0.050\pm 0.001 \,\mathrm{mm}\) ou \(e=50\pm 1 \,\mathrm{m}\)
Maus exemplos	\(B = (5.9297887668888668898\pm 0.08) 10^{-4} \,\mathrm{ T}\) \(Temp = 297\pm 0.0005\) \(q/m = (1.8\pm 0.07789) 10^{11}\,\mathrm{ C\cdot kg}^{-1}\)

Algarismos significativos

Com excepção do caso em que todos os números envolvidos são inteiros, não é possível representar o valor de uma grandeza com exactidão ilimitada. Diz-se que uma representação de um número tem \(n\) algarismos significativos quando se admite um erro na casa decimal seguinte. Por exemplo:

• 1/7 = 0,14 tem dois algarismos significativos
• 1/30 = 0,0333 tem três algarismos significativos

Note-se que a posição da vírgula não afecta o número de a.s.

Regras

• Algarismos zero à esquerda não contam para o total de a.s. – exemplo: 0,00044 ( 2 a.s.)
• Algarismos zero à direita contam para o total de a.s. – exemplo: 12,00 (4 a.s.)
• Algarismos 1–9 e zeros entre eles são sempre a.s. – exemplo: 1203,4 (5 a.s.)
• Potências de dez são ambíguas, e devem ser representadas usando notação decimal – exemplo: 800 é ambíguo, 8,00\(\times\)10\(^2\) é correcto (3 a.s.)
• As constantes têm um número arbitrário de a.s.

Soma e subtracção

O resultado deve manter o número de casas decimais do operando com o menor número de casas decimais

Exemplo: 105,4+0,2869+34,27 = 139,9569 = 140,0=1,400\(\times\)10\(^2\)

Multiplicação e divisão

O resultado deve manter o mesmo número de algarismos significativos do operando com o menor número de algarismos significativos.

Exemplo: 7,325\(\times\)8,14 = 59,6255 = 59,6

Raízes quadradas

O número de a.s. é igual ao de partida.

Exemplo: √92 = 9,59166 = 9,6

Incertezas nas representações gráficas: ajuste linear

A análise de resultados é frequentemente facilitada se se usarem representações gráficas das leis matemáticas que supostamente descrevem os fenómenos físicos em observação. O ajuste é particularmente simples se se tratar de uma lei linear, onde se pode fazer um ajuste visual.

De uma forma mais sistemática deve usar-se o método dos mínimos quadrados, que consiste na determinação analítica de qual a recta \(y=a+b\cdot x_i\) que se desvia o menos possível do conjunto de pontos experimentais. Na sua forma mais simples, sendo \((x_i,y_i)\) as coordenadas dos \(N\) pontos pretende-se determinar \((a,b)\) tal que

[math]\chi^2=\sum_{i=0}^N\left(y_i-y\right)^2=\sum_{i=0}^N\left(y_i-a-b \cdot x_i\right)^2[/math]

seja mínimo. As condições de estacionariedade desta função \(χ^2=F(a,b)\), dependente dos dois parâmetros \((a,b)\), podem ser descritas como \(\partial(χ^2)/\partial a=0,\partial(χ^2)/\partial b=0\) e \(\partial(χ^2)/\partial b^2=0\). As duas primeiras equações resultam em

[math] \begin{aligned} & \sum_{i=0}^N\left(y_i-a-b x_i\right)=0 \Leftrightarrow \sum y_i-N a-b \sum x_i=0 \\ & \sum_{i=0}^N x_i\left(y_i-a-b x_i\right)=0 \Leftrightarrow \sum x_i y_i-a \sum x_i-b \sum x_i^2=0 \end{aligned} [/math]

A resolução deste sistema de duas equações permite obter os valores de \(a\) e \(b\):

[math]a=\frac{\left(\sum x_i\right)^2 \sum y_i-\sum x_i \sum x_i y_i}{N \sum x_i^2-\left(\sum x_i\right)^2} \quad b=\frac{N \sum x_i y_i-\sum x_i \sum y_i}{N \sum x_i^2-\left(\sum x_i\right)^2}[/math]

A grande maioria dos programas de cálculo e as calculadoras científicas incorporam estas expressões para calcular os parâmetros de ajuste \(a\) e \(b\). Apenas os programas mais avançados para gráficos e análise de dados científicos (e.g Origin , Fitteia ou Qtiplot ) permitem também calcular as estimativas das incertezas \(u_a\) e \(u_b\).

Ajuste linear manual

É possível também obter um ajuste linear aproximado fazendo um traçado manual, com o rigor possível. Podemos usar como ponto de partida o ponto médio por onde passa a recta. Consideremos o sistema de duas equações acima; tomando a primeira e dividindo por \(N\),

[math]\frac{\sum y_i}{N}-a-b \frac{\sum x_i}{N}=0 \Leftrightarrow \bar{y}=a+b \bar{x}[/math]

em que \(\bar{y}\) e \(\bar{x}\) são respectivamente as médias de cada um dos conjuntos de valores. Daqui conclui-se que a recta que corresponde ao melhor ajuste passa pelo ponto médio \((\bar{x},\bar{y})\).

O passo seguinte consiste em traçar as rectas de maior \((y=a_1+b_1 x)\) e menor \((y=a_2+b_2 x)\) inclinação que, passando por este ponto, melhor se ajustam aos pontos medidos e suas incertezas. Por fim, a recta do melhor ajuste e o respectivo erro é obtida pela média desta duas rectas, de acordo com

[math]a=\frac{a_1+a_2}{2} \quad \varepsilon_a=\frac{\left|a_1-a_2\right|}{2} \quad b=\frac{b_1+b_2}{2} \quad \varepsilon_b=\frac{\left|b_1-b_2\right|}{2}[/math]

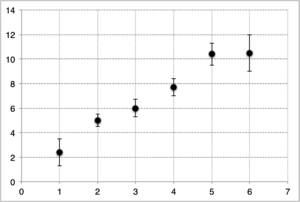
Exemplo: Considere-se o conjunto de pontos da tabela abaixo e a sua representação no gráfico.

\(x\) \(y\) \(\epsilon_y\) 1 2,4 1,1 2 5 0,5 3 6 0,7 4 7,7 0,8 5 10,4 0,9 6 10,5 1,5 Ponto médio: \(\bar{x}=3,5; \bar{y}=7,0\)

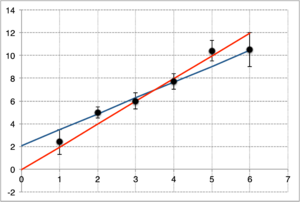
Traçamos duas rectas que passem pelo ponto médio (3,5; 7,0) e que correspondam visualmente (e com bom senso) ao maior e menor declive que contenham os pontos da medição.

Recta 1 (azul): \(y=1,4x+2,05\) Recta 2 (verm.): \(y=2,0x-0,05\)

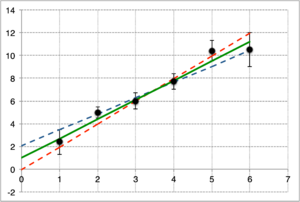
Por fim, calculam-se os coeficientes da recta que bissecta estas duas, dados pelas expressões acima.

Melhor ajuste: [math] \begin{align} a &=\frac{2,05+(-0,05)}{2}=1,0\\ ϵ_a &=\frac{|2,05-(-0,05)|}{2}=1,05\\ b &=\frac{1,4+2}{2}=1,7\\ ϵ_b &=\frac{|1,4-2}{2}=0,35 \end{align} [/math] Recta final (verde): \(y=1,7x+1,0\)

Como comparação, os valores calculados pelo método dos mínimos quadrados dão para a mesma recta o resultado \(y=1,67x+1,16\).

Bibliografia

• John R. Taylor, An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements, University Science Books; 2nd edition (August 1, 1996)
• V. Thomsen, Precision and The Terminology of Measurement. The Physics Teacher Vol. 35, pp.15-17, Jan. 1997.
• Ifan Hughes and Thomas Hase, Measurements and their Uncertainties: A practical guide to modern error analysis, Oxford University Press (July 1, 2010)