Diferenças entre edições de "Óptica Geométrica"
| (Há 64 edições intermédias do mesmo utilizador que não estão a ser apresentadas) | |||
| Linha 1: | Linha 1: | ||
<big>Construções geométricas em lentes delgadas</big> | <big>Construções geométricas em lentes delgadas</big> | ||
| + | |||
| + | {|class="wikitable" style="background-color:#ccddff;" | ||
| + | | Não consegue ver as equações correctamente? Mude https para http no endereço desta página e recarregue. | ||
| + | |} | ||
=Objectivos do trabalho= | =Objectivos do trabalho= | ||
| Linha 21: | Linha 25: | ||
|} | |} | ||
| − | |||
==Reflexão, refracção e polarização== | ==Reflexão, refracção e polarização== | ||
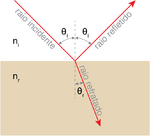
| − | + | [[file:OG-snell.png|thumb|upright=0.5 |Raio reflectido e refractado na fronteira entre dois meios. |Fig. 1 - Raio reflectido e refractado na fronteira entre dois meios.]] | |
A eficiência com que um feixe luminoso é reflectido ou refractado numa fronteira entre dois meios de índices de refracção \(n_1\)e \(n_2\) depende, entre outros, do ângulo de incidência e da polarização da luz. A Fig. 2 mostra como varia a reflectividade de uma superfície de vidro em função do ângulo de incidência, para polarizações horizontal e vertical (admitindo que o plano de incidência e reflexão é horizontal). Para um ângulo específico, designado [https://pt.wikipedia.org/wiki/%C3%82ngulo_de_Brewster ângulo de Brewster] e dado por \(\theta_B=\arctan(n_2/n_1)\), a componente horizontal da polarização não é reflectida, pelo que a luz reflectida fica com polarização vertical. Esta é uma forma de criar luz polarizada a partir de uma fonte não-polarizada. A figura ilustra também a geometria dos raios luminosos numa separação entre dois meios, no caso de incidência em ângulo de Brewster. Como se pode apreciar, nessa configuração o raio reflectido e o raio refractado fazem entre si um ângulo de 90\(^\circ\). | A eficiência com que um feixe luminoso é reflectido ou refractado numa fronteira entre dois meios de índices de refracção \(n_1\)e \(n_2\) depende, entre outros, do ângulo de incidência e da polarização da luz. A Fig. 2 mostra como varia a reflectividade de uma superfície de vidro em função do ângulo de incidência, para polarizações horizontal e vertical (admitindo que o plano de incidência e reflexão é horizontal). Para um ângulo específico, designado [https://pt.wikipedia.org/wiki/%C3%82ngulo_de_Brewster ângulo de Brewster] e dado por \(\theta_B=\arctan(n_2/n_1)\), a componente horizontal da polarização não é reflectida, pelo que a luz reflectida fica com polarização vertical. Esta é uma forma de criar luz polarizada a partir de uma fonte não-polarizada. A figura ilustra também a geometria dos raios luminosos numa separação entre dois meios, no caso de incidência em ângulo de Brewster. Como se pode apreciar, nessa configuração o raio reflectido e o raio refractado fazem entre si um ângulo de 90\(^\circ\). | ||
| − | Pode-se polarizar a luz emitida por uma fonte não-polarizada através de um simples [https://pt.wikipedia.org/wiki/Filtro_polarizador filtro polarizador] (ou ''polaroide''). Orientando o ângulo do filtro relativamente à direcção dos raios luminosos, é possível definir a direcção de polarização | + | Pode-se polarizar a luz emitida por uma fonte não-polarizada através de um simples [https://pt.wikipedia.org/wiki/Filtro_polarizador filtro polarizador] (ou ''polaroide''). Orientando o ângulo do filtro relativamente à direcção dos raios luminosos, é possível definir a direcção de polarização. Por exemplo, no caso da Fig. 3 a luz obtida é polarizada verticalmente. |
| − | [[file:OG-brewster.png|thumb|upright= | + | [[file:OG-brewster.png|thumb|upright=0.5 |Fig. 2 - Reflectividade vs. ângulo de incidência e direcção de polarização (esq.) e geometria para ângulo de Brewster (dir.).]] |
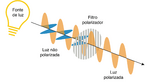
| − | [[file:OG-pol-luz.png|thumb|upright= | + | [[file:OG-pol-luz.png|thumb|upright=0.5 |Fig. 3 - Obtenção de luz polarizada através de um filtro polarizador.]] |
| − | =Construções geométricas em lentes delgadas= | + | = Construções geométricas em lentes delgadas= |
Uma das principais aplicações da óptica geométrica consiste no estudo da formação de imagens: dado um ''objecto'' numa dada posição, como desenhar um sistema óptico que permita transferir uma ''imagem'' desse objecto para uma posição diferente? É um problema que tem aplicações desde o olho humano até ao desenho de lentes e fibras ópticas. | Uma das principais aplicações da óptica geométrica consiste no estudo da formação de imagens: dado um ''objecto'' numa dada posição, como desenhar um sistema óptico que permita transferir uma ''imagem'' desse objecto para uma posição diferente? É um problema que tem aplicações desde o olho humano até ao desenho de lentes e fibras ópticas. | ||
| Linha 39: | Linha 42: | ||
Uma [https://pt.wikipedia.org/wiki/Lente '''lente'''] é um dos principais elementos usados em sistemas ópticos, e consiste tipicamente num sólido transparente com duas superfícies esféricas. Dependendo da curvatura destas superfícies, uma lente pode ser usada para aumentar ou diminuir o tamanho de um objecto, ou trazê-los objectos distantes para o ponto focal. As lentes são usadas por exemplo em óculos, câmaras, microscópios, telescópios e muitos outros sistemas de formação de imagem. | Uma [https://pt.wikipedia.org/wiki/Lente '''lente'''] é um dos principais elementos usados em sistemas ópticos, e consiste tipicamente num sólido transparente com duas superfícies esféricas. Dependendo da curvatura destas superfícies, uma lente pode ser usada para aumentar ou diminuir o tamanho de um objecto, ou trazê-los objectos distantes para o ponto focal. As lentes são usadas por exemplo em óculos, câmaras, microscópios, telescópios e muitos outros sistemas de formação de imagem. | ||
| − | Um objecto iluminado uniformemente é considerado como uma fonte de raios, emitidos em todas as direcções. Podemos escolher um ponto no objecto e um conjunto adequado de raios, e traçar o seu percurso através do sistema até encontrar o correspondente ponto na imagem. Por convenção, desenha-se o sistema óptico em torno de um eixo, que coincide com o seu eixo geométrico, e os raios propagam-se da esquerda para a direita. | + | Um objecto iluminado uniformemente é considerado como uma fonte de raios, emitidos em todas as direcções. Podemos escolher um ponto no objecto e um conjunto adequado de raios, e traçar o seu percurso através do sistema até encontrar o correspondente ponto na imagem. Por convenção, desenha-se o sistema óptico em torno de um eixo, que coincide com o seu eixo geométrico, e os raios propagam-se da esquerda para a direita. |
==Aproximações== | ==Aproximações== | ||
| − | Utilizaremos as duas seguintes aproximações comuns, que facilitam grandemente os cálculos a efectuar | + | [[file:OG-definicoes.png|thumb|upright=0.5 | Fig. 4 - Definições utilizadas.]] |
| + | Utilizaremos as duas seguintes aproximações comuns, que facilitam grandemente os cálculos a efectuar: | ||
{| class="wikitable" | {| class="wikitable" | ||
| '''Lentes delgadas''' || Uma lente é considerada ‘’delgada’’ quando a sua espessura \(d\) é desprezável face à sua [https://pt.wikipedia.org/wiki/Dist%C3%A2ncia_focal distância focal] \(f\). | | '''Lentes delgadas''' || Uma lente é considerada ‘’delgada’’ quando a sua espessura \(d\) é desprezável face à sua [https://pt.wikipedia.org/wiki/Dist%C3%A2ncia_focal distância focal] \(f\). | ||
| − | |||
|- | |- | ||
| '''Aproximação paraxial''' || Admitimos que todos os raios envolvidos são [https://pt.wikipedia.org/wiki/Aproxima%C3%A7%C3%A3o_paraxial paraxiais], isto é, (''i'') situam-se próximo do [https://pt.wikipedia.org/wiki/Eixo_%C3%B3ptico eixo óptico] e (''ii'') o ângulo \(\alpha\) que fazem com esse eixo permite utilizar as aproximações \(\sin \alpha \approx \alpha\) e \(\tan \alpha \approx \alpha\,\), tipicamente válidas para \(\alpha \lesssim 5^{\circ}\). | | '''Aproximação paraxial''' || Admitimos que todos os raios envolvidos são [https://pt.wikipedia.org/wiki/Aproxima%C3%A7%C3%A3o_paraxial paraxiais], isto é, (''i'') situam-se próximo do [https://pt.wikipedia.org/wiki/Eixo_%C3%B3ptico eixo óptico] e (''ii'') o ângulo \(\alpha\) que fazem com esse eixo permite utilizar as aproximações \(\sin \alpha \approx \alpha\) e \(\tan \alpha \approx \alpha\,\), tipicamente válidas para \(\alpha \lesssim 5^{\circ}\). | ||
|} | |} | ||
| − | + | A Fig. 4 ilustra a geometria relevante para estas definições, sendo \(f\) a distância focal, \(d\ll f\) a espessura da lente delgada e \(\alpha\) o ângulo entre o raio e o eixo óptico. | |
==Convenções== | ==Convenções== | ||
| Linha 75: | Linha 78: | ||
De seguida, vamos analisar a formação de imagens para lentes convergentes (\(f>0\)) e divergentes (\(f<0\)) em função da posição relativa do objecto e do foco da lente, e derivar relações úteis para lentes delgadas. | De seguida, vamos analisar a formação de imagens para lentes convergentes (\(f>0\)) e divergentes (\(f<0\)) em função da posição relativa do objecto e do foco da lente, e derivar relações úteis para lentes delgadas. | ||
| − | ==Objecto e imagem | + | ==Objecto e imagem: focos conjugados e ampliação transversal== |
Considere de novo a Fig. 5. Cada ponto do objecto em \(d_O\) tem um único ponto correspondente na imagem em \(d_I\). Isto implica que, caso colocássemos o objecto em \(d_I\), a imagem seria formada em \(d_O\). Chama-se a estas posições ''focos conjugados''. | Considere de novo a Fig. 5. Cada ponto do objecto em \(d_O\) tem um único ponto correspondente na imagem em \(d_I\). Isto implica que, caso colocássemos o objecto em \(d_I\), a imagem seria formada em \(d_O\). Chama-se a estas posições ''focos conjugados''. | ||
Pela semelhança de triângulos, temos as seguintes relações entre as dimensões do objecto e da imagem: | Pela semelhança de triângulos, temos as seguintes relações entre as dimensões do objecto e da imagem: | ||
| Linha 132: | Linha 135: | ||
===Imagem virtual=== | ===Imagem virtual=== | ||
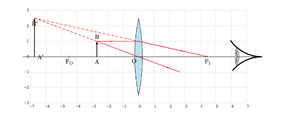
| − | + | [[file:OG-convvirt0.png|thumb|upright=1.0 |Fig. 6 - Formação de imagem virtual com uma lente convergente.]] | |
Este caso verifica-se quando \(d_O<f\), por exemplo quando utilizamos uma lupa para ver objectos com um tamanho aumentado, e está esquematizada na Fig. 6. Dependendo da posição \(d_O\), verificam-se as seguintes relações | Este caso verifica-se quando \(d_O<f\), por exemplo quando utilizamos uma lupa para ver objectos com um tamanho aumentado, e está esquematizada na Fig. 6. Dependendo da posição \(d_O\), verificam-se as seguintes relações | ||
| Linha 142: | Linha 145: | ||
Repare-se que resulta \(d_I<0\) (a imagem está do mesmo lado que o objecto) e \(A<0\) pelo que a imagem é (''i'') virtual e (''ii'') direita, para um observador colocado à direita da lente. | Repare-se que resulta \(d_I<0\) (a imagem está do mesmo lado que o objecto) e \(A<0\) pelo que a imagem é (''i'') virtual e (''ii'') direita, para um observador colocado à direita da lente. | ||
| − | + | ==Lente divergente (\(f<0\))== | |
| − | |||
[[file:OG-divvirt.png|thumb|upright=1.0 |Fig. 7 - Formação de imagem virtual com uma lente divergente.]] | [[file:OG-divvirt.png|thumb|upright=1.0 |Fig. 7 - Formação de imagem virtual com uma lente divergente.]] | ||
| − | + | [[file:OG-Ray-diagrams-types-lenses-length.png|thumb|upright=0.5 |Fig. 8 - Tabela resumo para lentes convergentes e divergentes.]] | |
| − | = | ||
Considere-se a situação representada na Fig. 7, que mostra uma lente divergente (\(f<0\)) e um objecto \(AB\) (\(d_O>0\)). Note-se que, no caso da lente divergente, os pontos \(F_O\)e \(F_I\) trocam de posição. Nesta configuração a imagem resultante \(A'B'\) é sempre ''virtual'' e ''direita'' com \(d_I <0\) (imagem do mesmo lado do objeto), pois | Considere-se a situação representada na Fig. 7, que mostra uma lente divergente (\(f<0\)) e um objecto \(AB\) (\(d_O>0\)). Note-se que, no caso da lente divergente, os pontos \(F_O\)e \(F_I\) trocam de posição. Nesta configuração a imagem resultante \(A'B'\) é sempre ''virtual'' e ''direita'' com \(d_I <0\) (imagem do mesmo lado do objeto), pois | ||
| Linha 163: | Linha 164: | ||
Nestas expressões, que descrevem distâncias, foi necessário utilizar os valores em módulo de \(f\) e de \(d_I\), que são ambos negativos. Fazendo agora as substituições \(|f|\to -f\) e \(|d_I|\to -d_I\) recupera-se a equação dos focos conjugados. | Nestas expressões, que descrevem distâncias, foi necessário utilizar os valores em módulo de \(f\) e de \(d_I\), que são ambos negativos. Fazendo agora as substituições \(|f|\to -f\) e \(|d_I|\to -d_I\) recupera-se a equação dos focos conjugados. | ||
| − | A Fig. | + | A Fig. 8 apresenta uma tabela resumo de todas as situações analisadas acima. |
| − | |||
| − | |||
==Objectos virtuais== | ==Objectos virtuais== | ||
| Linha 172: | Linha 171: | ||
===Lente convergente \(f>0\)=== | ===Lente convergente \(f>0\)=== | ||
| − | A Fig. | + | [[file:OG-convvirt.png|thumb|upright=1.0 |Fig. 9 - Lente convergente com objecto virtual e imagem real.]] |
| + | A Fig. 9 representa um objecto virtual (\(d_O<0\), à direita da lente) e a correspondente imagem. A imagem resultante é real (\(d_I>0\), também à direita) e direita (\(A<0\)), verificando-se | ||
\begin{array}{lcl} | \begin{array}{lcl} | ||
| Linha 178: | Linha 178: | ||
\frac{d_I}{-|d_O|} & =& \frac{f}{-|d_O| -f} | \frac{d_I}{-|d_O|} & =& \frac{f}{-|d_O| -f} | ||
\end{array} | \end{array} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===Lente divergente \(f<0\) - Imagem virtual=== | ===Lente divergente \(f<0\) - Imagem virtual=== | ||
| − | A Fig. | + | [[file:OG-divvirtvirt.png|thumb|upright=1.0 |Fig. 10 - Lente divergente com objecto virtual e imagem virtual.]] |
| + | A Fig. 10 representa um objecto virtual (\(d_O<0\), à direita da lente) para uma lente divergente (\(f<0\)) e a correspondente imagem. Na situação da figura, o objecto está à direita do foco \(F_O\): \(|d_O|>|f|\). Verifica-se assim: | ||
\begin{array}{lcl} | \begin{array}{lcl} | ||
| Linha 206: | Linha 202: | ||
===Lente divergente \(f>0\) - Imagem real=== | ===Lente divergente \(f>0\) - Imagem real=== | ||
| − | + | [[file:OG-divvirtreal.png|thumb|upright=1.0 |Fig. 11 - Lente divergente com objecto virtual e imagem real.]] | |
| − | A Fig. | + | A Fig. 11 representa um objecto virtual (\(d_O<0\), à direita da lente) para uma lente divergente (\(f<0\)) e a correspondente imagem. Na situação da figura, o objecto está à esquerda do foco \(F_O\): \(|d_O|<|f|\). Verifica-se assim: |
| − | |||
| − | |||
\begin{array}{lcl} | \begin{array}{lcl} | ||
| Linha 247: | Linha 241: | ||
==Lente convergente - lente convergente== | ==Lente convergente - lente convergente== | ||
| − | [[file:OG-duplaconvconv1.png|thumb|upright=1.0 |Sistema de duas lentes convergentes, com objecto intermédio real.]] | + | [[file:OG-duplaconvconv1.png|thumb|upright=1.0 |Fig. 12 - Sistema de duas lentes convergentes, com objecto intermédio real.]] |
| − | A Fig. | + | A Fig. 12 representa duas lentes convergentes, \(L_1\) e \(L_2\), de distâncias focais \(f_1\) e \(f_2\) respectivamente, separadas de uma distância \(D\). O objecto (real) \(AB\) situa-se à esquerda de \(L_1\), e tem uma imagem \(A'B'\) por intermédio de \(L_1\). Esta imagem constitui-se como objecto virtual para \(L_2\), resultando no final a imagem \(A^{\prime\prime}B^{\prime\prime}\). Esta é a montagem mais simples de um [https://pt.wikipedia.org/wiki/Telesc%C3%B3pio telescópio], a partir do qual se podem obter grandes ampliações. |
Apliquemos as equações de lentes individuais para cada caso: | Apliquemos as equações de lentes individuais para cada caso: | ||
| Linha 261: | Linha 255: | ||
</math> | </math> | ||
| − | [[file:OG-duplaconvconv2.png|thumb|upright=1.0 |Duas lentes convergentes, com objecto intermédio virtual.]] | + | [[file:OG-duplaconvconv2.png|thumb|upright=1.0 |Fig. 13 - Duas lentes convergentes, com objecto intermédio virtual.]] |
Estas três expressões permitem calcular o valor de uma das incógnitas, conhecidos os valores das outras. Por exemplo, uma aplicação comum desta montagem consiste em determinar o valor de uma distância focal desconhecida \(f_2\), conhecidos os valores de \(f_1\), \(d_{O_1}\), \(d_{I_2}\)e \(D\). | Estas três expressões permitem calcular o valor de uma das incógnitas, conhecidos os valores das outras. Por exemplo, uma aplicação comum desta montagem consiste em determinar o valor de uma distância focal desconhecida \(f_2\), conhecidos os valores de \(f_1\), \(d_{O_1}\), \(d_{I_2}\)e \(D\). | ||
| − | As mesmas expressões aplicam-se para o caso de uma imagem obtida por uma lente \(L_1\)que passa a ser um “objecto” virtual para \(L_2\), isto é, em que \(d_{O2}<0\), situação ilustrada na Fig. | + | As mesmas expressões aplicam-se para o caso de uma imagem obtida por uma lente \(L_1\)que passa a ser um “objecto” virtual para \(L_2\), isto é, em que \(d_{O2}<0\), situação ilustrada na Fig. 13. |
==Lente convergente - lente divergente== | ==Lente convergente - lente divergente== | ||
| − | O outro sistema de lente dupla de interesse é o caso em que temos uma lente convergente e uma divergente separadas de \(D\), ilustrado na Fig. | + | O outro sistema de lente dupla de interesse é o caso em que temos uma lente convergente e uma divergente separadas de \(D\), ilustrado na Fig. 14, em que \(L_1\) é convergente e \(L_2\) é divergente. A lente \(L_1\) produz uma imagem intermédia \(A'B'\) real e invertida, que é o objecto (real) de \(L_2\). Uma vez que a segunda lente é divergente, a sua imagem \(A^{\prime\prime}B^{\prime\prime}\) (a imagem final) é sempre virtual e invertida. |
| − | + | A Fig. 15 ilustra a situação em que \(A'B'\) está numa posição à direita de \(L_2\): é uma imagem real (de \(L_1\)) mas um objecto virtual (de \(L_2\)), já que \(d_{O2}<0\). A imagem \(A"B"\)resultante é real e invertida. | |
| − | + | Por fim, se nesta montagem permutarmos \(L_1\) e \(L_2\) (Fig. 16), obtém-se também uma imagem real \(A^{\prime\prime}\,B^{\prime\prime}\), desde que a distância \(d_{O1}=A\,O_1\) seja idêntica. Em qualquer destas situações, pode sempre calcular-se \(f_2 < 0\) usando o conjunto das três equações anteriores. | |
| − | [[file:OG- | + | {| class="wikitable" |
| − | + | | [[file:OG-duplaconvdiv1.png|thumb|upright=0.8 |Fig. 14 - Sistema de lente convergente e divergente com objecto intermédio real: a imagem final é virtual e invertida.]] || [[file:OG-duplaconvdiv2.png|thumb|upright=0.8 |Fig. 15 - Sistema de lente convergente e divergente com objecto intermédio virtual: a imagem final é real e invertida.]] || [[file:OG-duplaconvdiv3.png|thumb|upright=0.8 |Fig. 16 - Sistema de lente divergente e convergente.]] | |
| − | [[file:OG- | + | |} |
| − | |||
| − | |||
=Instrumentos ópticos= | =Instrumentos ópticos= | ||
| Linha 285: | Linha 277: | ||
==O olho humano== | ==O olho humano== | ||
| − | Vamos primeiro abordar a fisiologia do olho humano (Fig. | + | Vamos primeiro abordar a fisiologia do olho humano (Fig. 17) para compreender as suas limitações. Este pode ser considerado como um sistema óptico que projecta imagens (reais) dos objectos exteriores na retina, através de duas lentes convergentes: a córnea e o cristalino. Para o nosso estudo, vamos considerar que estas lentes são substituídas por um sistema equivalente constituído por uma única lente, com o máximo de distância focal \(f\) igual a 2,5 cm, que é a média da distância entre a córnea e a retina. A potência em dioptrias (dt) desta lente equivalente é dada por: |
<math display=“block”> | <math display=“block”> | ||
| Linha 291: | Linha 283: | ||
</math> | </math> | ||
| − | [[file:OG-olho-1.png|thumb|upright= | + | [[file:OG-olho-1.png|thumb|upright=0.5 |Fig. 17 - Diagrama dos principais elementos do olho humano.]] |
| + | Para uma pessoa com visão normal ou munida de correção adequada (óculos graduados ou lentes de contacto), os raios ópticos provenientes de um objecto no infinito<ref>Para efeitos práticos, considera-se o infinito óptico qualquer distância superior a 5 m.</ref> chegam paralelos ao olho e são focados na retina sem necessidade de esforço, ou seja, com o olho relaxado (Fig. 18 à esq.). À medida que o objecto se aproxima do olho, é necessário os músculos ciliares aumentarem a curvatura da lente para criar uma imagem focada na retina - a isto chama-se ''acomodação do olho''. O ponto mais próximo do olho para o qual a lente ainda consegue focar a imagem na retina é designado por ''ponto próximo'' (Fig. 18 à dir.) e considera-se igual a 0,25 m para uma visão normal padrão, valor que tem tendência a aumentar com a idade. | ||
| − | + | [[file:OG-olho-2.png|thumb|upright=1.0 |Fig. 18 - Esquema do olho no caso de objectos no infinito (esq.) e no ponto próximo (dir.).]] | |
| − | + | O tamanho aparente dum objecto é determinado pelo tamanho que a imagem apresenta na retina. Mesmo sem variar o tamanho real do objecto, este pode ser visto maior se o aproximarmos do olho, porque o tamanho da sua imagem na retina é maior. A avaliação do tamanho da imagem na retina pode ser feita através da medição do ângulo \(\theta\), que corresponde à inclinação dos raios principais do extremo da imagem (Fig. 19). | |
| − | + | [[file:OG-olho-3.png|thumb|upright=1.0 |Fig. 19 - Formação de imagem na retina de um objecto de altura \(h\)a uma distância \(s\).]] | |
| − | |||
| − | [[file:OG-olho-3.png|thumb|upright=1.0 |Formação de imagem na retina de um objecto de altura \(h\)a uma distância \(s\).]] | ||
Considere-se um objecto com altura \(h\) a uma distância \(s\) do olho. Para o objeto podemos escrever \(\tan\theta=h/s\). Para a imagem na retina, de altura \(y'\), vem \(\tan\theta = y'/\)(2,5 cm). Na aproximação paraxial, ou seja de ângulos pequenos, podemos usar \(\tan\theta \approx\theta\), e assim \(\theta\approx h/s=y'/\)(2,5 cm). Desta relação conclui-se que \(y'\) é proporcional a \(h\), tamanho do objecto, e inversamente proporcional à distância \(s\) entre o objecto e o olho. | Considere-se um objecto com altura \(h\) a uma distância \(s\) do olho. Para o objeto podemos escrever \(\tan\theta=h/s\). Para a imagem na retina, de altura \(y'\), vem \(\tan\theta = y'/\)(2,5 cm). Na aproximação paraxial, ou seja de ângulos pequenos, podemos usar \(\tan\theta \approx\theta\), e assim \(\theta\approx h/s=y'/\)(2,5 cm). Desta relação conclui-se que \(y'\) é proporcional a \(h\), tamanho do objecto, e inversamente proporcional à distância \(s\) entre o objecto e o olho. | ||
| Linha 307: | Linha 298: | ||
==Lupa== | ==Lupa== | ||
| − | + | [[file:OG-olho-4.png|thumb|upright=1.0 |Fig. 20 - Objecto no ponto próximo visto pelo olho desarmado.]] | |
| − | A lupa simples é o instrumento óptico mais elementar. Consiste numa só lente convergente e permite aumentar o tamanho aparente do objecto, ou seja, o tamanho da imagem na retina. Sabendo que a maior imagem que se pode obter dum objecto com o olho desarmado é quando o objecto está no ponto próximo (Fig. | + | A [https://pt.wikipedia.org/wiki/Lupa lupa simples] é o instrumento óptico mais elementar. Consiste numa só lente convergente e permite aumentar o tamanho aparente do objecto, ou seja, o tamanho da imagem na retina. Sabendo que a maior imagem que se pode obter dum objecto com o olho desarmado é quando o objecto está no ponto próximo (Fig. 20), e dado que \(y'_0\), tamanho da imagem na retina, é proporcional ao ângulo definido entre a altura do objecto \(h_0\)e a sua distância ao olho, pode-se escrever a relação |
<math display=“block”> | <math display=“block”> | ||
| Linha 315: | Linha 306: | ||
Na visão auxiliada pela lupa, esta é colocada perto do olho, e o objecto colocado a uma distância inferior ao foco. A imagem produzida pela lupa é virtual, ampliada e direita. | Na visão auxiliada pela lupa, esta é colocada perto do olho, e o objecto colocado a uma distância inferior ao foco. A imagem produzida pela lupa é virtual, ampliada e direita. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Ampliação angular== | == Ampliação angular== | ||
| − | + | [[file:OG-olho-5.png|thumb|upright=1.0 |Fig. 21 - Formação de imagem com o auxílio de uma lupa a uma distância \(b\)do olho. O objecto \(h_0\)está a uma distância \(d_O<f\)da lente, e a imagem (virtual) \(h'_a\)aparenta estar a uma distância \(d_i\)da lente e \(L\)do olho.]] | |
| − | A ''ampliação angular'' \(M_A\) dum instrumento óptico é determinada pela razão entre \(y'_a\), dimensão da imagem na retina quando o objecto é visto através do instrumento (Fig. | + | A ''ampliação angular'' \(M_A\) dum instrumento óptico é determinada pela razão entre \(y'_a\), dimensão da imagem na retina quando o objecto é visto através do instrumento (Fig. 21), e \(y'_0\), dimensão da imagem na retina quando vista pelo olho desarmado e o objecto no ponto próximo. A razão entre os respectivos ângulos permite esse cálculo, isto é |
<math display=“block”> | <math display=“block”> | ||
| Linha 338: | Linha 323: | ||
onde na última igualdade se recorreu à equação dos focos conjugados. Como a distância à imagem é negativa, \(d_i = - (L – b)\), obtém-se por fim | onde na última igualdade se recorreu à equação dos focos conjugados. Como a distância à imagem é negativa, \(d_i = - (L – b)\), obtém-se por fim | ||
| − | <math display=“block”> | + | {| class="wikitable" |
| + | | <math display=“block”> | ||
M_A = \frac{0,25}{L}\left(1+\frac{L–b}{f}\right) | M_A = \frac{0,25}{L}\left(1+\frac{L–b}{f}\right) | ||
</math> | </math> | ||
| + | |} | ||
| + | |||
Da análise desta expressão pode-se dizer que a ampliação diminui se \(L\) ou \(b\) aumentam. Existem três casos particulares de ampliação: | Da análise desta expressão pode-se dizer que a ampliação diminui se \(L\) ou \(b\) aumentam. Existem três casos particulares de ampliação: | ||
| − | + | {| class="wikitable" | |
| − | + | |- | |
| − | + | ! Caso !! Ampliação angular !! Interpretação | |
| − | \(M_A = \lim_{L\to\infty}\frac{0,25}{L}\left(1+\frac{L–b}{f}\right)= \frac{0,25}{f}=0,25D\). Neste caso, o olho recebe raios paralelos e não necessita de fazer acomodação, o que é mais cómodo, e a ampliação apenas se reduz de uma unidade relativamente ao caso | + | |- |
| − | + | | \(b=f\) || <center>\(M_A = \frac{0,25}{f}=0,25D\)</center> || O olho está à distância focal da lupa. \(D\) é a potência da lupa em dioptrias. | |
| − | Exemplo: uma lente com \(D=10\) dioptrias tem uma distância focal \(f=10\) cm, e para \(L=\infty\) tem uma ampliação de \(M_A=\)2,5 vezes. | + | |- |
| + | | \(b=0\) || <center>\(M_A = 0,25\left(\frac{1}{L}+\frac{1}{f}\right)\)</center> || O olho está encostado à lupa. Se \(b=0\) e também \(L = 0,25\) m (valor mínimo para \(L\), uma vez que a imagem também deve poder ser focada correctamente pelo olho), então obtém-se para \(M_A\) o valor máximo, igual a \(M_A = 1+\frac{0,25}{f}= 1+0,25D\). Neste caso, a imagem aumentada surge à distância do ponto próximo. | ||
| + | |- | ||
| + | | \(d_O=f\) || <center>\(M_A = \lim_{L\to\infty}\frac{0,25}{L}\left(1+\frac{L–b}{f}\right)\)\(= \frac{0,25}{f}=0,25D\)</center> || O objecto é colocado no foco e a lupa forma a sua imagem no infinito \((L = \infty)\). Neste caso, o olho recebe raios paralelos e não necessita de fazer acomodação, o que é mais cómodo, e a ampliação apenas se reduz de uma unidade relativamente ao caso anterior. | ||
| + | ''Exemplo'': uma lente com \(D=10\) dioptrias tem uma distância focal \(f=10\) cm, e para \(L=\infty\) tem uma ampliação angular de \(M_A=\)2,5 vezes. | ||
| + | |} | ||
==Microscópio composto== | ==Microscópio composto== | ||
| − | O [https://pt.wikipedia.org/wiki/Microsc%C3%B3pio_%C3%B3ptico microscópio] é o instrumento óptico empregado para observar objectos pequenos, colocados muito próximos do instrumento. Na sua forma mais simples, consiste em duas lentes convergentes. A lente mais próxima do objecto ([https://pt.wikipedia.org/wiki/Objetiva_(fotografia) objectiva]) tem uma distância focal \(f_{obj}\), menor que a distância focal \(f_{ocu}\) da lente mais perto do olho ([https://pt.wikipedia.org/wiki/Ocular ocular]) (Fig. | + | O [https://pt.wikipedia.org/wiki/Microsc%C3%B3pio_%C3%B3ptico microscópio] é o instrumento óptico empregado para observar objectos pequenos, colocados muito próximos do instrumento. Na sua forma mais simples, consiste em duas lentes convergentes. A lente mais próxima do objecto ([https://pt.wikipedia.org/wiki/Objetiva_(fotografia) objectiva]) tem uma distância focal \(f_{obj}\), menor que a distância focal \(f_{ocu}\) da lente mais perto do olho ([https://pt.wikipedia.org/wiki/Ocular ocular]) (Fig. 22). |
| − | [[file:OG-microscopio.png|thumb|upright=1.0 |Formação de imagem num microscópio.]] | + | [[file:OG-microscopio.png|thumb|upright=1.0 |Fig. 22 - Formação de imagem num microscópio.]] |
Um objecto de altura \(h\) é colocado, em relação à objectiva, mais afastado do que o foco desta, produzindo uma imagem de tamanho \(h'\) que é real, invertida e maior que o objecto. A objectiva produz assim uma imagem com ''ampliação transversal linear'' \(M_T\),<ref>Conforme vimos atrás, para o caso de uma única lente esta ampliação é designada \(A\).</ref> dada por: | Um objecto de altura \(h\) é colocado, em relação à objectiva, mais afastado do que o foco desta, produzindo uma imagem de tamanho \(h'\) que é real, invertida e maior que o objecto. A objectiva produz assim uma imagem com ''ampliação transversal linear'' \(M_T\),<ref>Conforme vimos atrás, para o caso de uma única lente esta ampliação é designada \(A\).</ref> dada por: | ||
| Linha 371: | Linha 364: | ||
</math> | </math> | ||
| + | =Procedimento experimental= | ||
==Material== | ==Material== | ||
Caixa de óptica equipada com | Caixa de óptica equipada com | ||
| − | + | * calha graduada | |
| − | + | * fonte luminosa com lâmpada de incandescência linear | |
| − | + | * lentes convergentes e divergente | |
| − | + | * semi-cilindro de vidro acrílico | |
| − | + | * diafragmas | |
| − | + | * polaroides | |
| − | + | * suportes | |
| − | |||
==Trabalho preparatório== | ==Trabalho preparatório== | ||
| Linha 394: | Linha 387: | ||
===Face plana=== | ===Face plana=== | ||
| − | + | # <li value="4">Monte o suporte com o círculo graduado e o semi-cilindro de vidro acrílico centrado, de modo a que o feixe de luz branca incida na sua superfície plana. Observe e obtenha os ângulos de reflexão e de transmissão para vários valores dos ângulos do feixe incidente, à esquerda e à direita. Registe medições para, pelo menos, nove valores diferentes do ângulo de incidência.</li> | |
| − | # Monte o suporte com o círculo graduado e o semi-cilindro de vidro acrílico centrado, de modo a que o feixe de luz branca incida na sua superfície plana. Observe e obtenha os ângulos de reflexão e de transmissão para vários valores dos ângulos do feixe incidente, à esquerda e à direita. Registe medições para, pelo menos, nove valores diferentes do ângulo de incidência. | ||
# Represente as medições num gráfico e, a partir deste, determine por ajuste o índice de refracção do vidro acrílico. Anexe o gráfico ao relatório. | # Represente as medições num gráfico e, a partir deste, determine por ajuste o índice de refracção do vidro acrílico. Anexe o gráfico ao relatório. | ||
===Face cilíndrica=== | ===Face cilíndrica=== | ||
| − | + | # <li value="6">Rode o círculo graduado de modo a que o feixe de luz incida na superfície cilíndrica do vidro acrílico. Repita as medidas e a análise dos resultados. | |
| − | # Rode o círculo graduado de modo a que o feixe de luz incida na superfície cilíndrica do vidro acrílico. Repita as medidas e a análise dos resultados. | ||
===Ângulo-limite=== | ===Ângulo-limite=== | ||
| − | + | # <li value="7">Estime o valor do índice de refracção a partir do ângulo limite de reflexão total. | |
| − | # Estime o valor do índice de refracção a partir do ângulo limite de reflexão total. | ||
# Para o desvio à exatidão, considere exato o valor médio das medições anteriores. | # Para o desvio à exatidão, considere exato o valor médio das medições anteriores. | ||
| − | # Nas suas conclusões, compare os valores obtidos para \(n_{vidro}\) e a sua precisão | + | # Nas suas conclusões, compare os valores obtidos para \(n_{vidro}\) e a sua precisão |
==Polarização da luz. Ângulo de Brewster== | ==Polarização da luz. Ângulo de Brewster== | ||
# Observe o efeito de interposição de dois filtros polarizadores, paralelos ou cruzados, no percurso de um feixe luminoso. | # Observe o efeito de interposição de dois filtros polarizadores, paralelos ou cruzados, no percurso de um feixe luminoso. | ||
# Usando a mesma montagem do ponto anterior, polarize o feixe paralelamente ao plano de incidência, orientando o eixo \(0^\circ-180^\circ\) do filtro polarizador na vertical. | # Usando a mesma montagem do ponto anterior, polarize o feixe paralelamente ao plano de incidência, orientando o eixo \(0^\circ-180^\circ\) do filtro polarizador na vertical. | ||
| − | # A partir do valor médio obtido para o índice de refracção (o que usou na secção anterior), calcule o valor "teórico" do ângulo de Brewster e verifique experimentalmente que, para esse valor, os raios reflectido e transmitido fazem 90 | + | # A partir do valor médio obtido para o índice de refracção (o que usou na secção anterior), calcule o valor "teórico" do ângulo de Brewster e verifique experimentalmente que, para esse valor, os raios reflectido e transmitido fazem 90\(^\circ\) entre si. |
| − | # Para ângulos de incidência próximos do ângulo de Brewster, obtenha o intervalo angular em que praticamente se extingue o feixe reflectido. | + | # Para ângulos de incidência próximos do ângulo de Brewster, obtenha o intervalo angular em que praticamente se extingue o feixe reflectido. |
==Distância focal de uma lente convergente ( \(f \approx\)75 mm)== | ==Distância focal de uma lente convergente ( \(f \approx\)75 mm)== | ||
| − | + | # Obtenha um feixe de luz branca de raios paralelos, usando a lente colimadora. | |
| − | # Seleccione a lente de distância focal mais curta e determine o seu valor pelo método directo. Repita a experiência duas vezes, colocando a lente | + | # Seleccione a lente de distância focal mais curta e determine o seu valor pelo método directo. Repita a experiência duas vezes, colocando a lente noutra posição relativamente à lente de raios paralelos. |
| − | noutra posição relativamente à lente de raios paralelos. | ||
# Retire a lente colimadora e coloque o objecto com mira no suporte da calha, iluminando-o directamente com a fonte luminosa. Coloque a mesma lente convergente a uma distância 150 mm \(> d_O >\)75 mm do objeto. | # Retire a lente colimadora e coloque o objecto com mira no suporte da calha, iluminando-o directamente com a fonte luminosa. Coloque a mesma lente convergente a uma distância 150 mm \(> d_O >\)75 mm do objeto. | ||
| − | + | # Com o écran plano, procure a posição correcta para obter uma imagem focada. Utilizando a equação dos focos conjugados, calcule de novo a d.f. da lente. | |
| − | # Com o écran plano, procure a posição correcta para obter uma imagem focada. | ||
| − | Utilizando a equação dos focos conjugados, calcule de novo a d.f. da lente. | ||
# Na folha quadriculada em anexo, desenhe um diagrama com o eixo óptico, o objecto e a lente convergente. Utilizando as aproximações paraxial e das lentes delgadas, desenhe a construção geométrica e obtenha a posição da imagem e a respectiva ampliação. | # Na folha quadriculada em anexo, desenhe um diagrama com o eixo óptico, o objecto e a lente convergente. Utilizando as aproximações paraxial e das lentes delgadas, desenhe a construção geométrica e obtenha a posição da imagem e a respectiva ampliação. | ||
| − | |||
# Medindo agora a imagem, determine a ampliação linear. Compare-a com a que podia calcular pelas distância \(d_O\) e \(d_I\). | # Medindo agora a imagem, determine a ampliação linear. Compare-a com a que podia calcular pelas distância \(d_O\) e \(d_I\). | ||
# Repita a experiência, colocando a lente noutra posição relativamente ao objecto. | # Repita a experiência, colocando a lente noutra posição relativamente ao objecto. | ||
| − | # Compare o valor da distância focal com o obtido em (1) e estime a precisão envolvida em | + | # Compare o valor da distância focal com o obtido em (1) e estime a precisão envolvida em cada um dos métodos que utilizou. |
| − | cada um dos métodos que utilizou | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | == Distância focal de uma lente divergente (\(f \approx -\)150 mm)== | ||
| + | # Associe no mesmo suporte a lente divergente com uma convergente (\(f \approx\)75 mm), de forma a que o par se comporte como um sistema convergente (com \(D\approx 10\)mm). Escolha uma distância ao objecto \(D_O\)adequada e utilize esta montagem para determinar a distância focal da lente divergente. | ||
| + | # Repita a montagem para uma diferente distância ao objecto. | ||
==Microscópio composto== | ==Microscópio composto== | ||
===Material=== | ===Material=== | ||
| − | + | * Lente objectiva \(f\)= 75 mm | |
| + | * Lente ocular \(f\)= 150 mm | ||
===Medição da ampliação angular da ocular=== | ===Medição da ampliação angular da ocular=== | ||
# Monte um ecrã graduado (E1) na parte lateral exterior de um suporte a \(d_i\approx 25\) cm da extremidade da calha, de modo a ficar no ponto próximo do observador. Este ecrã será a escala de referência, desempenhando o mesmo papel que a escala na parede, no caso do telescópio. | # Monte um ecrã graduado (E1) na parte lateral exterior de um suporte a \(d_i\approx 25\) cm da extremidade da calha, de modo a ficar no ponto próximo do observador. Este ecrã será a escala de referência, desempenhando o mesmo papel que a escala na parede, no caso do telescópio. | ||
| − | # Monte a lente ocular junto à mesma extremidade da calha, de modo a obter a condição \(b\sim 0\)(verifique a Fig. | + | # Monte a lente ocular junto à mesma extremidade da calha, de modo a obter a condição \(b\sim 0\) (verifique a Fig. 23). Calcule qual a distância \(d_O\) dessa lente a que deverá colocar um objecto (altura \(h_O\)) de modo a que a sua imagem surja no ponto próximo. Use o valor obtido para determinar a ampliação angular (calculada). |
| − | # Coloque outro ecrã graduado (E2) entre a lente e E1, próximo da posição \( | + | # Coloque outro ecrã graduado (E2) entre a lente e E1, próximo da posição \(d_O\) calculada acima, de modo a conseguir visualizar simultaneamente (a) a escala de E2 através da lente, com o olho esquerdo, e (b) a escala de E1 com o olho direito. |
| − | # Ajuste a posição de E2 até conseguir focar simultaneamente as imagens em ambos os olhos. Sobrepondo visualmente as duas escalas graduadas, meça o tamanho aparente \(h'_a\) da imagem (virtual) de E2 e determine a ampliação angular \(M_A\)da lente, usando a expressão adequada para | + | # Ajuste a posição de E2 até conseguir focar simultaneamente as imagens em ambos os olhos. Sobrepondo visualmente as duas escalas graduadas, meça o tamanho aparente \(h'_a\) da imagem (virtual) de E2 e determine a ampliação angular \(M_A\) da lente, usando a expressão adequada para este caso (ver Fig. 23 e consultar a tabela mais acima) |
| − | |||
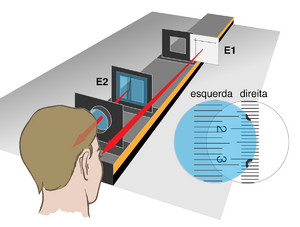
| − | [[file:OG-micro-composto.png|thumb|upright=1.0 |Esquema para a medição da ampliação angular da ocular.]] | + | [[file:OG-micro-composto.png|thumb|upright=1.0 |Fig. 23 - Esquema para a medição da ampliação angular da ocular.]] |
===Medição da ampliação linear da objectiva=== | ===Medição da ampliação linear da objectiva=== | ||
| − | + | # <li value="5">Mantendo a ocular montada e usando como referência a Fig. \ref{fig:microscopio}, junte uma objectiva e um objecto (um écran graduado iluminado). Escolha uma altura \(h_0\) adequada. | |
| − | # Mantendo a ocular montada e usando como referência a Fig. \ref{fig:microscopio}, junte uma objectiva e um objecto (um écran graduado iluminado). Escolha uma altura \(h_0\) adequada. | ||
# Se necessário, ajuste a objectiva para observar uma imagem focada através da ocular. | # Se necessário, ajuste a objectiva para observar uma imagem focada através da ocular. | ||
# Com um ecrã auxiliar, observe a imagem intermédia \(h’\) e meça a sua ampliação. | # Com um ecrã auxiliar, observe a imagem intermédia \(h’\) e meça a sua ampliação. | ||
# Calcule a ampliação final do microscópio composto. | # Calcule a ampliação final do microscópio composto. | ||
| + | |||
| + | =Notas= | ||
Edição atual desde as 15h01min de 11 de setembro de 2024
Construções geométricas em lentes delgadas
| Não consegue ver as equações correctamente? Mude https para http no endereço desta página e recarregue. |
Objectivos do trabalho
Pretende-se estudar vários aspectos da luz do ponto de vista da óptica geométrica, tais como a reflexão e refracção entre meios, a polarização, lentes delgadas e associações de lentes. Iremos estudar a formação de imagens reais e virtuais, verificar como estas dependem das distâncias envolvidas no sistema óptico, e testar um microscópio composto.
Conceitos fundamentais
Traçado de raios
A óptica geométrica, ou óptica de raios, é uma abordagem que consiste em descrever a propagação da luz através de raios. Um raio é um modelo simplificado, na forma de uma linha, que descreve o caminho percorrido pela luz entre duas superfícies. Para descrever a propagação de um feixe de luz através de um sistema, utilizamos um conjunto de raios, que se propagam utilizando o método do traçado de raios. Este método é suficiente para explicar fenómenos como a reflexão e a refracção da luz e é particularmente útil na descrição de sistemas e instrumentos ópticos, sendo válida desde que as dimensões dos objectos envolvidos sejam muito maiores que o comprimento de onda da luz visível (\(\sim\)0,4 \(\mu\)m a 0,7 \(\mu\)m).
O comportamento dos raios obedece a algumas regras simples:
|
Reflexão, refracção e polarização
A eficiência com que um feixe luminoso é reflectido ou refractado numa fronteira entre dois meios de índices de refracção \(n_1\)e \(n_2\) depende, entre outros, do ângulo de incidência e da polarização da luz. A Fig. 2 mostra como varia a reflectividade de uma superfície de vidro em função do ângulo de incidência, para polarizações horizontal e vertical (admitindo que o plano de incidência e reflexão é horizontal). Para um ângulo específico, designado ângulo de Brewster e dado por \(\theta_B=\arctan(n_2/n_1)\), a componente horizontal da polarização não é reflectida, pelo que a luz reflectida fica com polarização vertical. Esta é uma forma de criar luz polarizada a partir de uma fonte não-polarizada. A figura ilustra também a geometria dos raios luminosos numa separação entre dois meios, no caso de incidência em ângulo de Brewster. Como se pode apreciar, nessa configuração o raio reflectido e o raio refractado fazem entre si um ângulo de 90\(^\circ\).
Pode-se polarizar a luz emitida por uma fonte não-polarizada através de um simples filtro polarizador (ou polaroide). Orientando o ângulo do filtro relativamente à direcção dos raios luminosos, é possível definir a direcção de polarização. Por exemplo, no caso da Fig. 3 a luz obtida é polarizada verticalmente.
Construções geométricas em lentes delgadas
Uma das principais aplicações da óptica geométrica consiste no estudo da formação de imagens: dado um objecto numa dada posição, como desenhar um sistema óptico que permita transferir uma imagem desse objecto para uma posição diferente? É um problema que tem aplicações desde o olho humano até ao desenho de lentes e fibras ópticas.
Uma lente é um dos principais elementos usados em sistemas ópticos, e consiste tipicamente num sólido transparente com duas superfícies esféricas. Dependendo da curvatura destas superfícies, uma lente pode ser usada para aumentar ou diminuir o tamanho de um objecto, ou trazê-los objectos distantes para o ponto focal. As lentes são usadas por exemplo em óculos, câmaras, microscópios, telescópios e muitos outros sistemas de formação de imagem.
Um objecto iluminado uniformemente é considerado como uma fonte de raios, emitidos em todas as direcções. Podemos escolher um ponto no objecto e um conjunto adequado de raios, e traçar o seu percurso através do sistema até encontrar o correspondente ponto na imagem. Por convenção, desenha-se o sistema óptico em torno de um eixo, que coincide com o seu eixo geométrico, e os raios propagam-se da esquerda para a direita.
Aproximações
Utilizaremos as duas seguintes aproximações comuns, que facilitam grandemente os cálculos a efectuar:
| Lentes delgadas | Uma lente é considerada ‘’delgada’’ quando a sua espessura \(d\) é desprezável face à sua distância focal \(f\). |
| Aproximação paraxial | Admitimos que todos os raios envolvidos são paraxiais, isto é, (i) situam-se próximo do eixo óptico e (ii) o ângulo \(\alpha\) que fazem com esse eixo permite utilizar as aproximações \(\sin \alpha \approx \alpha\) e \(\tan \alpha \approx \alpha\,\), tipicamente válidas para \(\alpha \lesssim 5^{\circ}\). |
A Fig. 4 ilustra a geometria relevante para estas definições, sendo \(f\) a distância focal, \(d\ll f\) a espessura da lente delgada e \(\alpha\) o ângulo entre o raio e o eixo óptico.
Convenções
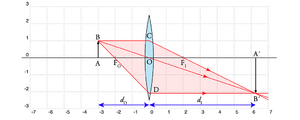
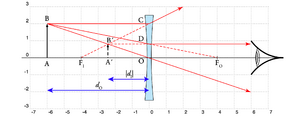
A Fig. 5 ilustra os principais parâmetros do traçado de raios através de uma lente simples.
- O objecto \(AB\) fica (por definição) do lado esquerdo da lente, a uma distância \(d_O>0\) desta; caso o objecto esteja do lado direito, temos \(d_O<0\) (que é o caso do objecto virtual abordado mais à frente)
- A imagem \(A'B'\) está do lado direito da lente, a uma distância \(d_I>0\) desta; caso a imagem esteja do lado esquerdo, temos \(d_I<0\)
- \(F_0\) é a distância focal do lado do objecto, \(F_I\) é a distância focal do lado da imagem. No caso de uma lente fina, ambas são iguais a \(f\), e marcam-se para auxiliar no traçado.
O raios ópticos que emergem de um dado objecto atravessam a lente e dão origem a uma imagem. A tabela em baixo descreve as propriedades dos dois tipos de imagens possíveis.
| Imagens reais | Os raios de luz passam de facto na posição da imagem, isto é, raios que saem do plano do objecto convergem no plano da imagem
Podem ser projectadas num alvo |
| Imagens virtuais | Os raios não passam na imagem, mas esta é visível através da lente
Não podem ser projectadas num alvo |
As imagens reais são, por exemplo, as criadas por um dispositivo de projecção. Um exemplo de imagem virtual é considerar a imagem de uma lâmpada brilhante: ao passar a mão pelo plano da imagem, se estar for real sente-se o calor, mas se for virtual parecerá apenas "flutuar" no espaço.
De seguida, vamos analisar a formação de imagens para lentes convergentes (\(f>0\)) e divergentes (\(f<0\)) em função da posição relativa do objecto e do foco da lente, e derivar relações úteis para lentes delgadas.
Objecto e imagem: focos conjugados e ampliação transversal
Considere de novo a Fig. 5. Cada ponto do objecto em \(d_O\) tem um único ponto correspondente na imagem em \(d_I\). Isto implica que, caso colocássemos o objecto em \(d_I\), a imagem seria formada em \(d_O\). Chama-se a estas posições focos conjugados. Pela semelhança de triângulos, temos as seguintes relações entre as dimensões do objecto e da imagem:
\begin{array}{lcl} \Delta ABF_O \sim \Delta ODF_O &\to & AB/A'B' = AF_O / F_O 0 &\to & AB/A'B' = \frac{d_O-f}{ f} \\ \Delta ABO\sim \Delta A'B'O &\to & AB/A'B' = AO / O A' &\to & AB/A'B' = d_O / d_I \\ \Delta COF_I \sim \Delta A'B'F_I &\to & AB/A'B' = OF_I / F_I A' &\to & AB/A'B' = \frac{f}{ d_I-f} \end{array}
Combinando a primeira e a última das expressões acima obtemos a equação dos focos conjugados:
| [math] \frac{1}{f} = \frac{1}{d_O} +\frac{1}{d_I} [/math] |
Uma forma alternativa e muitas vezes conveniente de exprimir esta relação consiste em utilizar as distâncias do objecto e da imagem aos respectivos focos. Designando estas distâncias por \(x_O=AF_O\) e \(x_I=A'F_I\), tem-se \(d_O=f+x_O\) e \(d_I=f+x_I\). Substituindo na expressão acima, obtém-se a chamada formulação de Newton para a equação dos focos conjugados:
| [math] x_Ox_I = f^2 [/math] |
Por outro lado, sendo \(AB\) e \(A'B'\)respectivamente as dimensões lineares transversais do objecto e da imagem, usamos a segunda das igualdades acima para definir a ‘’ampliação transversal’’ \(A\) como:
| [math] A = \frac{A'B'}{ AB} =\frac{d_I}{d_O} [/math] |
A imagem é ‘’direita’’ se \(A<0\) e ‘’invertida’’ se \(A>0\). Podemos usar estas duas equações para, dados \(f\)e \(d_O\), determinar as seguintes expressões para a posição da imagem \(d_I\)e a respectiva ampliação \(A\):
\begin{eqnarray} A&=&\frac{1}{\frac{d_O}{f}-1}\\ d_I&=&d_OA \end{eqnarray}
Como exemplo, temos no caso da Fig. 5: \(d_O>f \to A> 0\,; d_I > 0\). A imagem resultante é ‘’real’’ e ‘’invertida’’.
Lente convergente (\(f>0\))
Imagem real
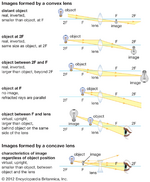
Este caso verifica-se para \(d_O>f\), a imagem é real é pode ser projectada. A imagem é menor (\(A<1\)) que o objecto se \(d_O>2f\) ou maior (\(A>1\)) se \(2f>d_O>0\). Um exemplo do primeiro caso é uma máquina fotográfica: a imagem é posicionada no sensor da câmara, e é (tipicamente) menor que o objecto fotografado. Verifica-se \(0 < A \le 1\) pois
[math] \infty \gt d_O \ge 2 f \quad \to \quad f \lt d_I \le 2 f \quad \to \quad 0 \lt A\le 1 [/math]
Um exemplo do segundo caso é um projetor de cinema ou de imagem de computador: a imagem é posicionada num écran, e é maior que o objecto (película ou chip). Verifica-se \(1 \le A < \infty\) pois
[math] f \lt d_O \le 2 f \quad \to \quad \infty \gt d_I \ge 2f \quad \to \quad \infty \gt A\ge 1 [/math]
Imagem virtual
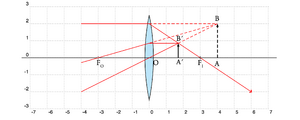
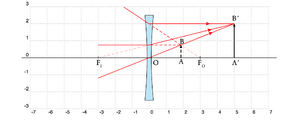
Este caso verifica-se quando \(d_O<f\), por exemplo quando utilizamos uma lupa para ver objectos com um tamanho aumentado, e está esquematizada na Fig. 6. Dependendo da posição \(d_O\), verificam-se as seguintes relações
\begin{array}{lcl} 0 < d_O \le \frac{f}{2} \qquad & 0 > d_I \ge -f \quad& -1 >A \ge -2\\ \frac{f}{2} \le d_O < f \qquad& -f\ge d_I >-\infty \quad& -2 > A > -\infty \end{array}
Repare-se que resulta \(d_I<0\) (a imagem está do mesmo lado que o objecto) e \(A<0\) pelo que a imagem é (i) virtual e (ii) direita, para um observador colocado à direita da lente.
Lente divergente (\(f<0\))
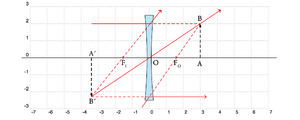
Considere-se a situação representada na Fig. 7, que mostra uma lente divergente (\(f<0\)) e um objecto \(AB\) (\(d_O>0\)). Note-se que, no caso da lente divergente, os pontos \(F_O\)e \(F_I\) trocam de posição. Nesta configuração a imagem resultante \(A'B'\) é sempre virtual e direita com \(d_I <0\) (imagem do mesmo lado do objeto), pois
[math] f\lt0; \quad d_O\gt 0 \quad \to \quad A\lt0; \quad d_I \lt0 [/math]
Podemos verificar que a equação dos focos conjugados se mantém válida neste caso, recorrendo à semelhança de triângulos:
\begin{array}{lcl} \Delta ABO \sim \Delta A'B'O & \to & AB/A'B' = \frac{d_0}{d_I} & \to & -\infty < A < 0 \\ \Delta ABF_0\sim \Delta ODF_O &\to & \frac{d_0 + |f|}{|f|} = AB/A'B' & \to & \frac{d_0 + |f|}{|f|} = \frac{d_0 }{d_I} \\ \Delta F_I OC \sim \Delta F_I A'B' &\to & \frac{|f|}{|f| - |d_I|} =AB/A'B' & \to & \frac{|f|}{|f| - |d_I|} = \frac{d_0 }{|d_I|} \end{array}
Nestas expressões, que descrevem distâncias, foi necessário utilizar os valores em módulo de \(f\) e de \(d_I\), que são ambos negativos. Fazendo agora as substituições \(|f|\to -f\) e \(|d_I|\to -d_I\) recupera-se a equação dos focos conjugados.
A Fig. 8 apresenta uma tabela resumo de todas as situações analisadas acima.
Objectos virtuais
Em determinadas situações, podemos lidar com objectos virtuais (\(d_O<0\)), isto é, os raios ópticos têm origem não num objecto sólido, mas num plano do espaço, e estamos interessados em estudar a sua propagação a partir desse plano e a formação da imagem correspondente. Um exemplo típico consiste em estudar a formação da imagem de uma imagem primária. Nestes casos, o objecto virtual é identificado a tracejado no diagrama de raios, como ilustrado nos exemplos em baixo.
Lente convergente \(f>0\)
A Fig. 9 representa um objecto virtual (\(d_O<0\), à direita da lente) e a correspondente imagem. A imagem resultante é real (\(d_I>0\), também à direita) e direita (\(A<0\)), verificando-se
\begin{array}{lcl} d_O < 0 ; \quad && f > 0 \quad \to \quad A<0\\ \frac{d_I}{-|d_O|} & =& \frac{f}{-|d_O| -f} \end{array}
Lente divergente \(f<0\) - Imagem virtual
A Fig. 10 representa um objecto virtual (\(d_O<0\), à direita da lente) para uma lente divergente (\(f<0\)) e a correspondente imagem. Na situação da figura, o objecto está à direita do foco \(F_O\): \(|d_O|>|f|\). Verifica-se assim:
\begin{array}{lcl} d_O < 0 & & f < 0 \\ \frac{d_I}{|d_O|} & =& \frac{|f|}{|d_O| -|f|} \end{array}
A imagem resultante é também virtual \(d_I<0\), à esquerda da lente) e invertida (\(A>0\)), verificando-se as seguintes relações em função da distância:
[math] |d_O| = \left\{ \begin{array}{rl} |d_O| = |f|: & |d_I| \to \infty, \quad A \to \infty ,\\ |f| \lt |d_O| \lt 2|f|: & |d_I| \gt |d_O| , \quad A \gt1 ,\\ |d_O| = 2|f|: & |d_I| = |d_O|, \quad A =1 ,\\ |d_O| \gt 2|f|: & |d_I| \lt|d_O| , \quad 0 \lt A \lt1 . \end{array} \right. %f\lt0 \quad \to d_O\gt 0 ; \quad d_I \lt0 [/math]
Lente divergente \(f>0\) - Imagem real
A Fig. 11 representa um objecto virtual (\(d_O<0\), à direita da lente) para uma lente divergente (\(f<0\)) e a correspondente imagem. Na situação da figura, o objecto está à esquerda do foco \(F_O\): \(|d_O|<|f|\). Verifica-se assim:
\begin{array}{lcl} d_O < 0 & & f < 0 \nonumber\\ \frac{d_I}{|d_O|} & =& \frac{|f|}{|f|-|d_O|} \quad \to \quad A=\frac{d_I}{d_O} =\frac{f}{d_O-f}<0 \nonumber \end{array}
A imagem resultante é agora real (\(d_I>0\), à direita da lente) e direita (\(A<0\)), verificando-se as seguintes relações em função da distância:
[math] |d_O| = \left\{ \begin{array}{rl} |d_O| \to |f|: & |d_I| \to \infty, \quad A \to -\infty ,\\ |d_O| = |f|/2: & |d_I| = f, \quad A =-2 ,\\ |d_O| =0: & |d_I| =0 , \quad A=-1. \end{array} \right. %f\lt0 \quad \to d_O\gt 0 ; \quad d_I \lt0 [/math]
Associação de lentes delgadas
Para duas lentes delgadas de distâncias focais \(f_1\)e \(f_2\) afastadas de \(D\) (para \(D \ll f_1,f_2\)) pode calcular-se a distância focal equivalente do conjunto através de:
| [math] \frac{1}{f_{equiv}} = \frac{1}{f_1} + \frac{1}{f_2} - \frac{D}{f_1 \,f_2} [/math] |
A dificuldade na determinação da distância focal equivalente \({f_{equiv}}\) é a medição das distâncias \(d_O\) e \(d_I\) (que são diferentes das distância do objecto e da imagem às superfícies das lentes ou aos seus planos médios).
Uma abordagem preferível consiste em usar a equação dos focos conjugados separadamente para cada uma das lentes, e considerar que a primeira imagem (real ou virtual) irá constituir-se como o objecto para a segunda lente. Neste caso, as regras descritas acima para o traçado de raios de lentes individuais aplicam-se consecutivamente:
- A partir da posição do objecto \(AB\) e do tipo da primeira lente \(L_1\), determina-se a posição da imagem intermédia \(A'B'\)
- A partir da posição da imagem intermédia (agora tomada como objecto da segunda lente) e do tipo da segunda lente \(L_2\), determina-se a posição da imagem final \(A^{\prime\prime}B^{\prime\prime}\)
Vamos aplicar este método para várias combinações de lentes convergentes e divergentes.
Lente convergente - lente convergente
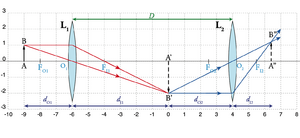
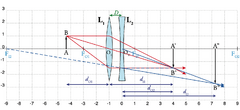
A Fig. 12 representa duas lentes convergentes, \(L_1\) e \(L_2\), de distâncias focais \(f_1\) e \(f_2\) respectivamente, separadas de uma distância \(D\). O objecto (real) \(AB\) situa-se à esquerda de \(L_1\), e tem uma imagem \(A'B'\) por intermédio de \(L_1\). Esta imagem constitui-se como objecto virtual para \(L_2\), resultando no final a imagem \(A^{\prime\prime}B^{\prime\prime}\). Esta é a montagem mais simples de um telescópio, a partir do qual se podem obter grandes ampliações. Apliquemos as equações de lentes individuais para cada caso:
[math] |d_O| = \left\{ \begin{array}{llll} \frac{1}{d_{O_1}} + \frac{1}{d_{I_1}} = \frac{1}{f_1} & d_{O_1} = AO_1 & d_{I_1} = O_1A' & f_1 = O_1 F_{O_1} = O_1\,F_{I_1} \\ \frac{1}{d_{O_2}} + \frac{1}{d_{I_2}} = \frac{1}{f_2} & d_{O_2} = A'O_2 & d_{I_2} = O_2\,A'' & f_2 = F_{O_2}\,O_2\, = O_2\,F_{I_2} \\ O_1\,O_2 = D = d_{I_1} + d_{O_2} \end{array} \right. \label{eq:assoclentes_2} [/math]
Estas três expressões permitem calcular o valor de uma das incógnitas, conhecidos os valores das outras. Por exemplo, uma aplicação comum desta montagem consiste em determinar o valor de uma distância focal desconhecida \(f_2\), conhecidos os valores de \(f_1\), \(d_{O_1}\), \(d_{I_2}\)e \(D\).
As mesmas expressões aplicam-se para o caso de uma imagem obtida por uma lente \(L_1\)que passa a ser um “objecto” virtual para \(L_2\), isto é, em que \(d_{O2}<0\), situação ilustrada na Fig. 13.
Lente convergente - lente divergente
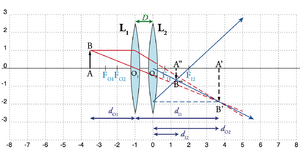
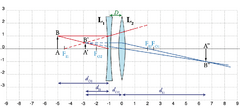
O outro sistema de lente dupla de interesse é o caso em que temos uma lente convergente e uma divergente separadas de \(D\), ilustrado na Fig. 14, em que \(L_1\) é convergente e \(L_2\) é divergente. A lente \(L_1\) produz uma imagem intermédia \(A'B'\) real e invertida, que é o objecto (real) de \(L_2\). Uma vez que a segunda lente é divergente, a sua imagem \(A^{\prime\prime}B^{\prime\prime}\) (a imagem final) é sempre virtual e invertida.
A Fig. 15 ilustra a situação em que \(A'B'\) está numa posição à direita de \(L_2\): é uma imagem real (de \(L_1\)) mas um objecto virtual (de \(L_2\)), já que \(d_{O2}<0\). A imagem \(A"B"\)resultante é real e invertida.
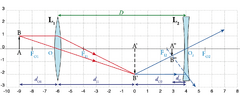
Por fim, se nesta montagem permutarmos \(L_1\) e \(L_2\) (Fig. 16), obtém-se também uma imagem real \(A^{\prime\prime}\,B^{\prime\prime}\), desde que a distância \(d_{O1}=A\,O_1\) seja idêntica. Em qualquer destas situações, pode sempre calcular-se \(f_2 < 0\) usando o conjunto das três equações anteriores.
Instrumentos ópticos
Um instrumento óptico é um dispositivo baseado nos princípios da óptica cujo objectivo é auxiliar a visão humana. Nestes sistemas, designamos por objectiva a lente que está do lado do objeto AB e por ocular aquela que está do lado do observador, com distâncias focais \(f_{obj}\) e \(f_{ocu}\) respetivamente. Em ambos os casos, a ocular está próxima da imagem intermédia A'B' formada pela objectiva. Sendo a distância inferior à distância focal \(f_{ocu}\), a imagem final será virtual, ou seja, visível apenas através da lente. Assim, o papel da ocular consiste em ampliar a imagem intermédia, tal como uma lupa amplia um objeto.
O olho humano
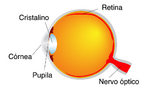
Vamos primeiro abordar a fisiologia do olho humano (Fig. 17) para compreender as suas limitações. Este pode ser considerado como um sistema óptico que projecta imagens (reais) dos objectos exteriores na retina, através de duas lentes convergentes: a córnea e o cristalino. Para o nosso estudo, vamos considerar que estas lentes são substituídas por um sistema equivalente constituído por uma única lente, com o máximo de distância focal \(f\) igual a 2,5 cm, que é a média da distância entre a córnea e a retina. A potência em dioptrias (dt) desta lente equivalente é dada por:
[math] D=\frac{1}{f} \,[\mathrm{m}^{-1}] = \frac{1}{0,025} \,[\mathrm{m}^{-1}] = 40 \,[\mathrm{m}^{-1}]=40\, \mathrm{dt}. [/math]
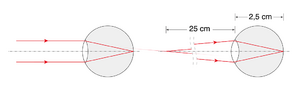
Para uma pessoa com visão normal ou munida de correção adequada (óculos graduados ou lentes de contacto), os raios ópticos provenientes de um objecto no infinito[1] chegam paralelos ao olho e são focados na retina sem necessidade de esforço, ou seja, com o olho relaxado (Fig. 18 à esq.). À medida que o objecto se aproxima do olho, é necessário os músculos ciliares aumentarem a curvatura da lente para criar uma imagem focada na retina - a isto chama-se acomodação do olho. O ponto mais próximo do olho para o qual a lente ainda consegue focar a imagem na retina é designado por ponto próximo (Fig. 18 à dir.) e considera-se igual a 0,25 m para uma visão normal padrão, valor que tem tendência a aumentar com a idade.
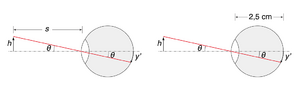
O tamanho aparente dum objecto é determinado pelo tamanho que a imagem apresenta na retina. Mesmo sem variar o tamanho real do objecto, este pode ser visto maior se o aproximarmos do olho, porque o tamanho da sua imagem na retina é maior. A avaliação do tamanho da imagem na retina pode ser feita através da medição do ângulo \(\theta\), que corresponde à inclinação dos raios principais do extremo da imagem (Fig. 19).
Considere-se um objecto com altura \(h\) a uma distância \(s\) do olho. Para o objeto podemos escrever \(\tan\theta=h/s\). Para a imagem na retina, de altura \(y'\), vem \(\tan\theta = y'/\)(2,5 cm). Na aproximação paraxial, ou seja de ângulos pequenos, podemos usar \(\tan\theta \approx\theta\), e assim \(\theta\approx h/s=y'/\)(2,5 cm). Desta relação conclui-se que \(y'\) é proporcional a \(h\), tamanho do objecto, e inversamente proporcional à distância \(s\) entre o objecto e o olho.
O princípio dos instrumentos ópticos consiste no aumento do tamanho da imagem na retina, \(y'\), permitindo assim visualizar objectos muito pequenos ou afastados. Do exposto acima, podemos concluir que a sua operação baseia-se na criação de uma imagem (real ou virtual) com um tamanho aparente maior que \(h\) e/ou a uma distância aparente inferior a \(s\). Em qualquer dos casos, a imagem final produzida deverá estar situada além do ponto próximo, caso contrário não conseguirá ser focada.
Lupa
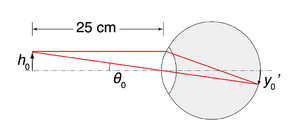
A lupa simples é o instrumento óptico mais elementar. Consiste numa só lente convergente e permite aumentar o tamanho aparente do objecto, ou seja, o tamanho da imagem na retina. Sabendo que a maior imagem que se pode obter dum objecto com o olho desarmado é quando o objecto está no ponto próximo (Fig. 20), e dado que \(y'_0\), tamanho da imagem na retina, é proporcional ao ângulo definido entre a altura do objecto \(h_0\)e a sua distância ao olho, pode-se escrever a relação
[math] \theta_0=h_0/0,25 [/math]
Na visão auxiliada pela lupa, esta é colocada perto do olho, e o objecto colocado a uma distância inferior ao foco. A imagem produzida pela lupa é virtual, ampliada e direita.
Ampliação angular
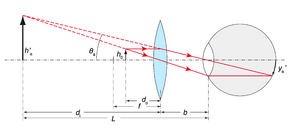
A ampliação angular \(M_A\) dum instrumento óptico é determinada pela razão entre \(y'_a\), dimensão da imagem na retina quando o objecto é visto através do instrumento (Fig. 21), e \(y'_0\), dimensão da imagem na retina quando vista pelo olho desarmado e o objecto no ponto próximo. A razão entre os respectivos ângulos permite esse cálculo, isto é
[math] M_A=\frac{y'_a}{y'_0}=\frac{\theta_a}{\theta_0} [/math]
Tirando partido da aproximação paraxial, temos \(\tan\theta_a = h'_a / L \approx \theta_a\) e \(\tan\theta_0 = h_0 / 0,25 \approx\theta_0\), portanto pode-se escrever a ampliação angular como:
[math] M_A = \frac{h'_a/L}{h_0/0,25}=-\frac{d_i\,0,25}{d_0 L}= \frac{0,25}{L}\left(1-\frac{d_i}{f}\right) [/math]
onde na última igualdade se recorreu à equação dos focos conjugados. Como a distância à imagem é negativa, \(d_i = - (L – b)\), obtém-se por fim
| [math] M_A = \frac{0,25}{L}\left(1+\frac{L–b}{f}\right) [/math] |
Da análise desta expressão pode-se dizer que a ampliação diminui se \(L\) ou \(b\) aumentam. Existem três casos particulares de ampliação:
| Caso | Ampliação angular | Interpretação |
|---|---|---|
| \(b=f\) | O olho está à distância focal da lupa. \(D\) é a potência da lupa em dioptrias. | |
| \(b=0\) | O olho está encostado à lupa. Se \(b=0\) e também \(L = 0,25\) m (valor mínimo para \(L\), uma vez que a imagem também deve poder ser focada correctamente pelo olho), então obtém-se para \(M_A\) o valor máximo, igual a \(M_A = 1+\frac{0,25}{f}= 1+0,25D\). Neste caso, a imagem aumentada surge à distância do ponto próximo. | |
| \(d_O=f\) | O objecto é colocado no foco e a lupa forma a sua imagem no infinito \((L = \infty)\). Neste caso, o olho recebe raios paralelos e não necessita de fazer acomodação, o que é mais cómodo, e a ampliação apenas se reduz de uma unidade relativamente ao caso anterior.
Exemplo: uma lente com \(D=10\) dioptrias tem uma distância focal \(f=10\) cm, e para \(L=\infty\) tem uma ampliação angular de \(M_A=\)2,5 vezes. |
Microscópio composto
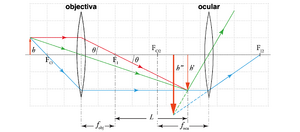
O microscópio é o instrumento óptico empregado para observar objectos pequenos, colocados muito próximos do instrumento. Na sua forma mais simples, consiste em duas lentes convergentes. A lente mais próxima do objecto (objectiva) tem uma distância focal \(f_{obj}\), menor que a distância focal \(f_{ocu}\) da lente mais perto do olho (ocular) (Fig. 22).
Um objecto de altura \(h\) é colocado, em relação à objectiva, mais afastado do que o foco desta, produzindo uma imagem de tamanho \(h'\) que é real, invertida e maior que o objecto. A objectiva produz assim uma imagem com ampliação transversal linear \(M_T\),[2] dada por:
[math] M_T=\frac{h'}{h} = -\frac{L\tan\theta}{f_{obj}\tan\theta}= -\frac{L}{f_{obj}} [/math]
O sinal negativo indica que a imagem é invertida e, uma vez que é real, a imagem pode ser projectada sobre um alvo para se medir o seu tamanho.
A lente ocular é usada para aumentar a imagem formada pela lente objectiva. Assim, a ocular é colocada de modo a que a imagem \(h'\) produzida pela objectiva (agora objecto virtual da segunda lente) venha localizar-se a uma distância ligeiramente inferior ao seu foco \(f_{ocu}\). Nesta condição, a ocular actua como uma simples lupa, que permite trazer o objecto \(h’\) para uma distância mais curta do que o ponto próximo (0,25 m), e produz a imagem \(h"\). A ampliação final \(M\) é dada pelo produto da ampliação transversal para a lente objectiva e a ampliação angular \(M_A\) obtida para a lente ocular. No caso da lente ocular estar encostada ao olho, como é habitual num microscópio, estamos no caso \(b=0\) e, das expressões anteriores para a ampliação linear e angular, obtemos
[math] M = \frac{h''}{h}=M_T\times M_A [/math]
Procedimento experimental
Material
Caixa de óptica equipada com
- calha graduada
- fonte luminosa com lâmpada de incandescência linear
- lentes convergentes e divergente
- semi-cilindro de vidro acrílico
- diafragmas
- polaroides
- suportes
Trabalho preparatório
- Preencha os objectivos do trabalho que irá realizar na sessão de laboratório.
- Preencha o quadro com as equações necessárias para o cálculo das grandezas, bem como as suas incertezas.
Determinação do índice de refracção dum vidro acrílico
Alinhamento
- Monte a fonte luminosa numa das extremidades da calha graduada e ligue a lâmpada.
- Utilizando uma lente, obtenha um feixe de luz branca de raios paralelos. De que tipo de lente necessita?
- Com os diafragmas, obtenha um feixe de luz estreito (\(\approx\)1 mm), alinhado com o eixo da calha graduada. Verifique que a espessura do feixe de luz se mantém tão constante quanto possível ao longo de toda a calha.
Face plana
- Monte o suporte com o círculo graduado e o semi-cilindro de vidro acrílico centrado, de modo a que o feixe de luz branca incida na sua superfície plana. Observe e obtenha os ângulos de reflexão e de transmissão para vários valores dos ângulos do feixe incidente, à esquerda e à direita. Registe medições para, pelo menos, nove valores diferentes do ângulo de incidência.
- Represente as medições num gráfico e, a partir deste, determine por ajuste o índice de refracção do vidro acrílico. Anexe o gráfico ao relatório.
Face cilíndrica
- Rode o círculo graduado de modo a que o feixe de luz incida na superfície cilíndrica do vidro acrílico. Repita as medidas e a análise dos resultados.
Ângulo-limite
- Estime o valor do índice de refracção a partir do ângulo limite de reflexão total.
- Para o desvio à exatidão, considere exato o valor médio das medições anteriores.
- Nas suas conclusões, compare os valores obtidos para \(n_{vidro}\) e a sua precisão
Polarização da luz. Ângulo de Brewster
- Observe o efeito de interposição de dois filtros polarizadores, paralelos ou cruzados, no percurso de um feixe luminoso.
- Usando a mesma montagem do ponto anterior, polarize o feixe paralelamente ao plano de incidência, orientando o eixo \(0^\circ-180^\circ\) do filtro polarizador na vertical.
- A partir do valor médio obtido para o índice de refracção (o que usou na secção anterior), calcule o valor "teórico" do ângulo de Brewster e verifique experimentalmente que, para esse valor, os raios reflectido e transmitido fazem 90\(^\circ\) entre si.
- Para ângulos de incidência próximos do ângulo de Brewster, obtenha o intervalo angular em que praticamente se extingue o feixe reflectido.
Distância focal de uma lente convergente ( \(f \approx\)75 mm)
- Obtenha um feixe de luz branca de raios paralelos, usando a lente colimadora.
- Seleccione a lente de distância focal mais curta e determine o seu valor pelo método directo. Repita a experiência duas vezes, colocando a lente noutra posição relativamente à lente de raios paralelos.
- Retire a lente colimadora e coloque o objecto com mira no suporte da calha, iluminando-o directamente com a fonte luminosa. Coloque a mesma lente convergente a uma distância 150 mm \(> d_O >\)75 mm do objeto.
- Com o écran plano, procure a posição correcta para obter uma imagem focada. Utilizando a equação dos focos conjugados, calcule de novo a d.f. da lente.
- Na folha quadriculada em anexo, desenhe um diagrama com o eixo óptico, o objecto e a lente convergente. Utilizando as aproximações paraxial e das lentes delgadas, desenhe a construção geométrica e obtenha a posição da imagem e a respectiva ampliação.
- Medindo agora a imagem, determine a ampliação linear. Compare-a com a que podia calcular pelas distância \(d_O\) e \(d_I\).
- Repita a experiência, colocando a lente noutra posição relativamente ao objecto.
- Compare o valor da distância focal com o obtido em (1) e estime a precisão envolvida em cada um dos métodos que utilizou.
Distância focal de uma lente divergente (\(f \approx -\)150 mm)
- Associe no mesmo suporte a lente divergente com uma convergente (\(f \approx\)75 mm), de forma a que o par se comporte como um sistema convergente (com \(D\approx 10\)mm). Escolha uma distância ao objecto \(D_O\)adequada e utilize esta montagem para determinar a distância focal da lente divergente.
- Repita a montagem para uma diferente distância ao objecto.
Microscópio composto
Material
- Lente objectiva \(f\)= 75 mm
- Lente ocular \(f\)= 150 mm
Medição da ampliação angular da ocular
- Monte um ecrã graduado (E1) na parte lateral exterior de um suporte a \(d_i\approx 25\) cm da extremidade da calha, de modo a ficar no ponto próximo do observador. Este ecrã será a escala de referência, desempenhando o mesmo papel que a escala na parede, no caso do telescópio.
- Monte a lente ocular junto à mesma extremidade da calha, de modo a obter a condição \(b\sim 0\) (verifique a Fig. 23). Calcule qual a distância \(d_O\) dessa lente a que deverá colocar um objecto (altura \(h_O\)) de modo a que a sua imagem surja no ponto próximo. Use o valor obtido para determinar a ampliação angular (calculada).
- Coloque outro ecrã graduado (E2) entre a lente e E1, próximo da posição \(d_O\) calculada acima, de modo a conseguir visualizar simultaneamente (a) a escala de E2 através da lente, com o olho esquerdo, e (b) a escala de E1 com o olho direito.
- Ajuste a posição de E2 até conseguir focar simultaneamente as imagens em ambos os olhos. Sobrepondo visualmente as duas escalas graduadas, meça o tamanho aparente \(h'_a\) da imagem (virtual) de E2 e determine a ampliação angular \(M_A\) da lente, usando a expressão adequada para este caso (ver Fig. 23 e consultar a tabela mais acima)
Medição da ampliação linear da objectiva
- Mantendo a ocular montada e usando como referência a Fig. \ref{fig:microscopio}, junte uma objectiva e um objecto (um écran graduado iluminado). Escolha uma altura \(h_0\) adequada.
- Se necessário, ajuste a objectiva para observar uma imagem focada através da ocular.
- Com um ecrã auxiliar, observe a imagem intermédia \(h’\) e meça a sua ampliação.
- Calcule a ampliação final do microscópio composto.