Cálculo de volume de revolução
Metadata
- CONTEXTO : Primeiro ciclo universitário
- AREA: Matemática
- DISCIPLINA: Calculo Diferencial e Integral 2
- ANO: 1
- LINGUA: pt
- AUTOR: Ana Moura Santos e Miguel Dziergwa
- MATERIA PRINCIPAL: Aplicações ao cálculo de grandezas físicas
- DESCRICAO: Cálculo de volume de um sólido de revolução
- DIFICULDADE: **
- TEMPO MEDIO DE RESOLUCAO: 15 mn
- TEMPO MAXIMO DE RESOLUCAO: 30 mn
- PALAVRAS CHAVE: função integrável à Riemann, integral como soma de áreas circulares
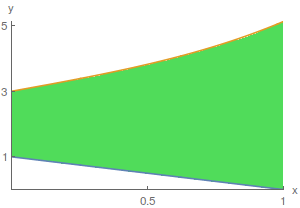
Na figura abaixo está representada a região compreendida entre os gráficos das funções \(f\) e \(g\), no intervalo \( [0,1] \), sendo as funções dadas por \(\pmb{\text{f(x)=}}\pmb{1-x}\) e \(\pmb{\text{g(x)=}}\pmb{\sinh\left(\frac{3x}{2}\right)+3}\).
O volume do sólido obtido quando se faz a revolução desta região em torno do eixo dos xx é igual a:
A)\(\pmb{\frac{1}{6}\pi\left(25+\sinh(3)+24\cosh\left(\frac{3}{2}\right)\right)}\)
B)\(\pmb{\frac{1}{36}\pi^2\left(11+4\cosh\left(\frac{3}{2}\right)\right)^2}\)
C)\(\pmb{\frac{1}{6}\pi\left(29+\sinh(3)+24\cosh\left(\frac{3}{2}\right)\right)}\)
D)\(\pmb{\frac{1}{6}\left(11+4\cosh\left(\frac{3}{2}\right)\right)}\)
Para obter o zip que contém as instâncias deste exercício clique aqui(volumesRevolucao)
Se deseja obter o código fonte que gera os exercícios contacte miguel.dziergwa@ist.utl.pt